网络神经科学与连接组学革命

要理解一个复杂系统的行为，我们需要理解该系统的各个元素在孤立状态下的行为，以及它们之间的相互作用和由它们的集体相互作用产生的模式多样性。人类大脑就是这样一个复杂系统。它帮助我们感知和理解我们的环境，创造（有时也会遗忘）记忆，甚至在培养创造力方面发挥作用。这些行为是由我们的神经系统支持的，神经系统由细胞、神经元群和大脑区域组成。然而，思维并非源自这些单独的神经元素。相反，复杂行为是由相互作用的神经元素创造的分布式解剖和功能网络所产生的。要理解思维，我们必须首先理解大脑网络的结构和功能。
从历史上看，神经科学主要关注可以定位到单个神经元素的神经系统属性，例如皮层区域的血氧水平依赖性（BOLD）活动或其曲率和沟回。然而，最近研究的重点已经转向分布式网络的属性。这种观点的转变很大程度上是由于网络科学的成熟，它为数学表达和分析高维数据集提供了框架，并已成功应用于其他学科。
这两个事件，加上数据共享计划和获得高性能计算机的机会，帮助创建了一个“连接组学革命”，在这个革命中，神经科学（特别是使用MRI方法的人类神经影像学）开始从网络的角度明确研究大脑的结构和功能。今天，生成大脑网络的程序已经基本自动化，并且网络分析正在解决关于大脑组织的神经科学基本问题，以及它在健康和疾病中的功能，具有精湛的细节和个性化。
本文涵盖了连接组学和网络神经科学的基本原则，重点关注大规模人类神经影像学。首先，我们介绍功能性和结构性连接的概念，并概述从观察中重建这些类型数据的过程。然后，我们讨论如何将这些数据建模为一个复杂网络，强调生物神经网络的网络模型揭示了大脑组织或功能的关键见解的三种方式：结构-功能关系、大脑网络动力学和大脑系统级架构。最后，我们涉及连接组学中的一些前沿话题，重点关注生成模型、网络可控性和基于边的方法。本文发表在Connectomic Deep Brain Stimulation一书。(可添加微信号siyingyxf或18983979082获取原文，另思影提供免费文献下载服务，如需要也可添加此微信号入群，原文也会在群里发布)。

温故而知新，建议结合以下脑网络相关解读阅读,另思影可承接相关数据处理业务（直接点击，即可浏览，加微信siyingyxf或18983979082获取原文及补充材料或咨询相关业务）：

连接组学揭示了单相抑郁症中大脑活动的改变

大脑模块化：和干预相关认知可塑性的生物标志物

电生理连接组学

PFC网络在认知控制和执行功能中的作用

从静息态和任务态的大数据中发现动态大脑网络

网络神经科学的统计功效

额顶网络：功能、电生理和个体精准定位的重要性

功能脑网络在神经退行性疾病患者中的评估

脑部疾病功能网络组织的图论方法

脑连接组学（PET）

静息状态fMRI功能连通性网络中的比例阈值的选择

现代物理评论：大脑网络中的动力学控制

重放，默认模式网络和记忆的级联系统控制网络和hubs

Nature Neuroscience：网络神经科学

PNAS：节食可调节年轻人脑网络的稳定性

复杂大脑网络的结构和功能

脑功能网络重建的原理与有待解决的问题

人脑的连接性中心节点促进了人脑网络的模块化 大脑状态的重构与认知行为之间的映射 大脑是一种什么样的网络? 大尺度功能脑组织结构：6个主要原则

从宏观尺度脑网络的角度看结构--功能关系

图论在静息态和动态脑连接评估中的应用：构建脑网络的方法

脑网络组织的经济性

儿童神经认知网络的动态功能连接 动态功能连接：前景、问题和解释Nature reviews Neuroscience：认知加工相关的默认网络自闭症研究中的默认网络默认网络：最新的解剖、生理研究及其研究发展过程中的新观点

DMN:大脑的默认网络

脑网络核心节点的发育

抑郁症，神经影像学和连接组学

重度抑郁症多成像中心的泛化脑网络标志物

Biological Psychiatry：精分患者大脑的组织体积变化与脑网络

Neuron：从简单映射到多维网络

脑网络视角下的精神分裂症

基于人脑连接组学将疾病症状映射于脑网络

大脑连接障碍中跨脑疾病的连接图论在识别人脑网络连通性模式中的应用

结构性和功能性大脑网络

大脑网络是告诉我们哪些神经元素相互连接、哪些没有连接以及每个连接的强度或效能的地图。尽管这些地图可以在所有空间尺度上创建，从细胞到区域，但连接组学在宏观尺度上已经得到认可并显示出特别具有变革性，最小的神经元素是体素，每个体素大约包含106个神经元（尽管在实践中，根据一组共享特征，体素会聚集成更大的区块或感兴趣区域）。大脑中的两个区域或区块相互作用意味着什么？总的来说，该领域已经确定了大脑两部分可以相互作用的三种不同“类型”或模式。

连接性的种类

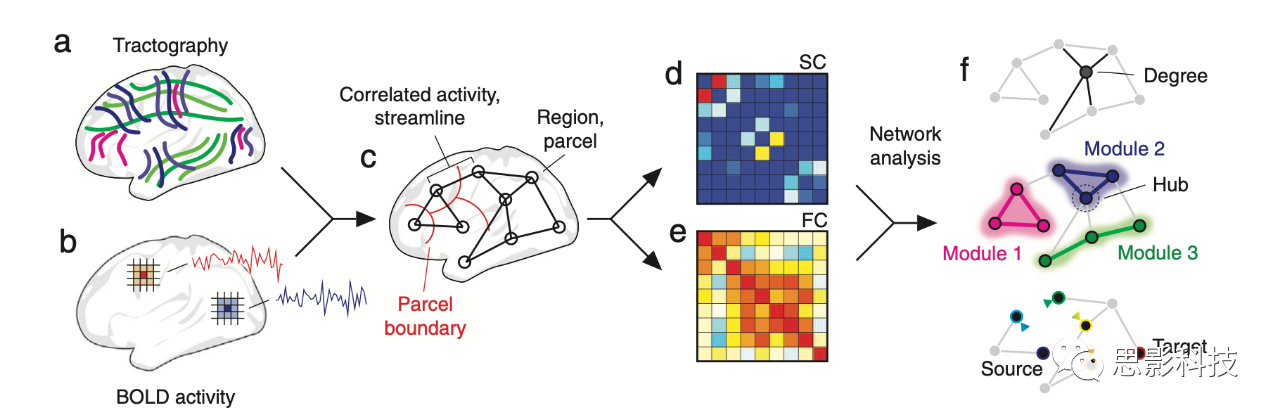
SHAPE \* MERGEFORMAT

图 2.1 构建、表征和分析大脑网络。大脑网络通常由扩散加权和功能性磁共振成像数据构建。(a) 对于扩散磁共振成像，tractography（纤维束追踪法）用于推断白质通路。

(b) 对于功能磁共振成像，连接性通常定义为来自体素或表面顶点的BOLD时间序列之间的统计依赖性。

(c) 大脑通常被划分为不同的区块或区域，使得每个区块在内部具有相似特征的体素/顶点组成的同质性。通过根据区块聚合连接权重，生成区域间的结构和功能连接矩阵（d和e）。通常，结构连接（SC）是稀疏的，其连接由纤维束计数、分数各向异性或相关测量加权。功能连接（FC）是完全加权的，在Pearson相关的情况下，带有符号。(f) SC和FC的网络表征随后可以进行分析，例如使用局部、中观和全局尺度的网络度量。
互动的第一个衡量标准是解剖学上的或结构性连接（SC），描述了大脑的物理和材料路径。在微观和中观尺度上，SC反映了细胞间的突触耦合或神经元群间的长距离轴突投射。在宏观尺度上，SC对应于大的、髓鞘化的白质纤维束。这些束可以通过扩散加权MRI数据重建，该数据测量大脑中水分子扩散的显现方向，使用一种称为“纤维追踪”的过程，许多软件包能够高效实现这个过程（见第11章）（图2.1a）。

实际上，SC限制了哪些神经元素可以相互“交流”，塑造信号模式和信息流动，并在神经元素对之间引起统计依赖性及其记录活动。这些依赖关系被称为功能连接（FC），原则上可以使用任何双变量统计相似性测量进行量化。这些测量包括谱或小波相干性、互信息、偏相关性和惩罚相关性等。然而，在实践中，当使用功能性MRI数据时，大脑区域之间的FC几乎总是被测量为它们活动的双变量（皮尔逊）相关性（见第10章和第16章）。

当然，还有其他测量神经元素之间互动性的方法。这些包括有效连接（EC），提供了动态因果建模、Granger因果关系和传递熵等方法，这些方法测量一个神经元素对另一个神经元素的有向影响。通常情况下，估计神经元素连接之间的真实因果关系是具有挑战性的，需要实验操控，例如观察对其他神经元素活动的扰动的影响，或者一个关于如何将活动从大脑的一个部分传递到另一个部分的特定模型，通常受到SC的约束。侵入性手段如深部脑刺激在EC背景下具有特别的前景，因为它们为绘制神经元素之间的因果关系提供了独特的机会，并验证现有的因果模型。

其他不太常见的用于估计神经元素之间互动强度的方法包括它们的结构协方差，它测量区域形态特征的群体水平相似性（尽管最近的进展已经使得为单个受试者估计类似指标成为可能）。

表征大脑连接

为了分析大脑连接性模式，我们需要一种数学方法来表征这些模式。我们可以借助图论来实现这一目标，图论是研究网络的数学分支。如第1章所述，图是网络的数学表示，包括两个基本成分：一组顶点或节点，表示系统的基本单元；一组边或连接，表示节点对之间的相互作用。例如，在社交系统中，如Twitter这样的在线社区，节点代表用户，边表示一个用户是否关注另一个用户。对于大脑来说，节点和边通常分别表示大脑区域及其结构或功能连接（图2.1c）。尽管图的最简单版本是二进制的、无向的——即所有边具有相同的权重并编码对称关系——但图也可以编码关于连接权重和不对称性的信息（那些是和不是相互作用的）。

无论网络是加权/二进制的，还是有向/无向的，其节点之间的成对关系都可以表示为邻接矩阵或连接矩阵。该方阵中行数和列数等于网络中节点的数量，其元素表示连接的存在或不存在以及权重。在SC矩阵中，权重通常对应于流线计数（成对区块之间重建的流线数）、密度或流线的微结构属性，例如，它们的分数各向异性（图2.1d）。尽管SC矩阵中的连接密度可能因处理流程而异，但结构网络通常是稀疏的，这意味着实际存在的连接相对较少。如前所述，功能连接表示双变量统计依赖性度量，导致一个完全加权且带符号的矩阵（图2.1e）。

在准备连接矩阵时需要谨慎，推断功能和SC的过程是复杂的，容易出现假阳性和假阴性。因此，在后处理步骤中通常需要对观察到的连接施加某种阈值，以保留具有最强权重的连接或最不可能表示假阳性的连接。然而，值得注意的是，阈值化通常并非必要；在某些情况下，保留所有连接可能是有益的。无论如何，阈值化与否的决定都是非常重要的，将对网络后续分析产生影响。在任何情况下，都可以使用图论网络度量进一步分析阈值化或未阈值化的连接矩阵，以概括网络组织的不同方面。

网络度量和分析

网络的邻接矩阵简洁地描述了其拓扑结构——节点之间连接的配置。大脑网络的分析通常涉及研究不同拓扑尺度上的连接矩阵，范围从局部测量的单个大脑区域和连接到描述整个大脑的全局特性。这些度量通常从网络功能的角度进行解释。在本节中，我们描述了一些在连接矩阵上可以进行的更常见的测量，并提供一些解释。

局部度量

局部度量描述了单个节点和边的属性。例如，一个节点的度仅计算该节点建立的输入和输出连接的数量。尽管简单，节点的度是可以为网络计算的最基本的度量之一，影响其他局部属性。具有许多连接的节点——潜在的“枢纽”区域——在网络中往往占据有影响力和重要性的位置。

中心性度量量化了节点或边相对于网络上进行的动态过程或网络的其他结构特征的重要性。最常见的度量之一是介数中心性，它计算包含给定节点的节点对之间最短路径的数量。在网络中，最短路径是从源节点到目标节点的最短跳跃序列，将在下一节中详细讨论。通过统计涉及给定连接的最短路径数量，也可以计算网络边的介数中心性。当然，还有其他中心性度量可以衡量节点和边相对于网络其他过程和结构的重要性，例如随机游走和社区。

重要的是，大多数局部度量都可以为二进制、加权、有向和无向网络计算。例如，节点度的加权类似物是节点强度，它测量与给定节点相连的所有连接的总权重。类似地，节点的介数中心性可以基于节点间的最短加权路径来计算。

全局度量

与局部度量相反，全局度量量化了网络整体的属性。例如，网络的最短路径结构可用于计算一些常见的全局网络度量，包括特征路径长度，它测量最短路径中的平均步数。这种度量具有重要的功能后果——在运输网络中，货物或信息从一个节点传递到另一个节点，较短的路径意味着传输效率的提高。在神经系统的背景下，大脑区域需要相互沟通，较短的路径意味着更快的传输时间和更少的信号衰减、变形或其他减弱的机会。

特征路径长度是一个无界度量，这使得很难比较不同大小的网络。如果网络由断开的组件组成，它还可能产生一个无穷大的值（两个断开的节点之间的路径长度是无限的）。为了避免这些问题，可以计算相关的全局效率度量。与特征路径长度是所有节点之间的平均最短路径不同，效率等于平均最短路径的倒数（1除以最短路径的长度）。因此，任何断开连接且具有无限路径长度的节点现在具有0的效率（1/∞）。效率度量限制在[0, 1]的区间内。

值得注意的是，路径长度和效率可以从二进制网络（其中最短路径对应于跳数或步数）扩展到加权网络。然而，需要小心。用于映射最短路径的算法试图最小化一个成本函数——路径上的步数或总权重。然而，在大脑网络中，连接权重通常衡量连接的亲和性或强度——从起始点到目标的最有效路径是使用强连接权重的路径。因此，可以计算加权最短路径，但需要将连接权重从亲和性度量转换为长度的中间步骤。这通常通过对边缘权重进行负指数运算（即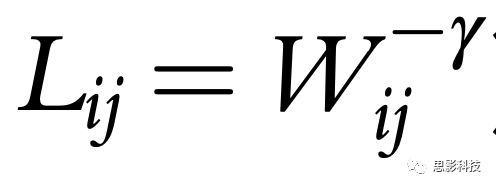，）或者通过将边缘权重除以其最大值并取负对数（即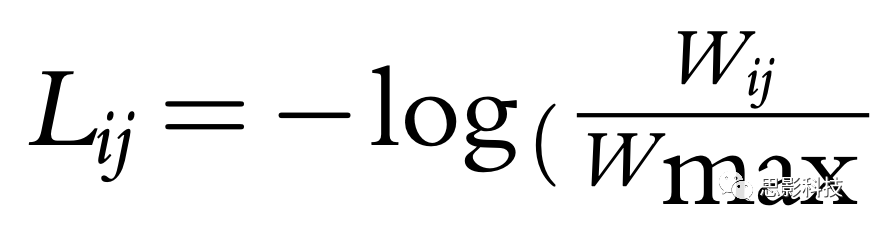，）来实现。这些转换以单调的方式将权重映射到长度，因此较大的权重必然对应较小的长度。

中尺度度量

位于局部和全局尺度之间的丰富中尺度。局部和全局网络属性描述节点和边缘或整个网络的特征，而中尺度度量关注大网络内子网络的属性，这些属性被认为支持专门的脑功能。在网络科学的术语中，这些子网络或集群被称为模块或“社区”，参考社交网络，其中社区代表个体群。中尺度结构分析可以说是网络科学最活跃的领域之一，它用于模式发现、功能组识别、网络粗粒化以及生成其他局部和全局网络统计数据。

然而，除了一些简单的例子，网络的中尺度结构事先是未知的，仅凭视觉检查无法确定。相反，中尺度结构是通过一系列“社区检测”算法以算法方式检测的。这些算法旨在将网络的节点或边划分为社区，通常是非重叠的。网络神经科学中最流行的方法是模块度最大化和 Infomap，它们寻求节点的划分，以优化各自的目标函数。

中尺度本身跨越多个组织层次，从网络划分为单个社区（每个节点都是自己的社区）到整个网络被分配到同一集群。像模块度最大化这样的方法可以参数化调整以检测特定大小的社区（类似于Infomap的最新版本）。

一旦检测到网络的社区结构，就可以使用它来计算其他局部和全局网络度量。例如，用于优化模块度最大化的目标函数Q可以用作衡量网络社区彼此隔离程度的指标。同样，我们可以从单个节点或脑区的角度观察社区，并使用像参与系数这样的度量来考虑它们在模块内外的连接分布，这些度量与其伙伴度量模块度z得分一起，可以用来推断节点是否充当中心节点，以及其影响是否超越了自身模块。例如，具有大参与系数的节点具有跨越模块边界的连接，位于调解模块间流量的位置。

我们从中学到了什么？

网络神经科学和连接组学为从网络视角研究大脑的组织提供了定量框架。采用这些方法的研究正在揭示功能和结构大脑网络的组织，阐明它们在健康和疾病中的运作。例如，与大多数现实世界的网络一样，大脑呈现出小世界架构，这意味着它们具有高度的局部聚类以支持专门的处理，但也具有拓扑“捷径”以减少最短路径的平均长度，支持快速传输大脑中的信息。其他研究表明，大脑网络表现出异质的度分布，这意味着少数大脑区域比其他区域建立更多的连接。这些潜在的“中心”节点占据有影响力的位置，并相互连接，形成一个所谓的“富人俱乐部”，由具有高度影响力的大脑区域组成。有趣的是，富人俱乐部节点分布在大脑的功能系统中，这表明这些相互连接的中心位于整合不同子系统和模态信息的位置。

尽管现代连接组学是多方面的，包括许多活跃的研究领域，无论是应用还是理论，在接下来的部分中，我们将讨论三个特别有影响力的主题。这些主题包括将大脑的组织分为功能专门化的子系统，阐明结构和功能连接之间的联系，以及跟踪随时间变化的功能网络架构。

系统级组织

大多数现实世界的网络都表现出一定程度的中尺度结构，这样节点和边可以有意义地划分为子网络、模块和社区。然而，这些社区的特性可能有所不同。例如，网络的社区结构可以形成一个密集的核心和稀疏的外围，或者甚至表现出非同质的多部分结构，其中子网络由内部连接稀疏的节点组成，但在组间存在许多强连接。然而，最常见的中尺度组织类型是同质的模块结构，其中节点被安排成内部密集连接的子网络，但彼此之间的连接较弱。实际上，模块结构在现实世界的网络中无处不在，发展新方法来检测和描述这些类型的社区仍是网络科学研究的一个活跃领域。

大脑是否具有模块化？为什么我们期望大脑呈现模块化组织？具有模块的大脑是否具有模块化大脑所缺乏的某种优势？

模块化网络的一个关键特征是模块之间的近乎自治，这使得它们能够发展出专门的认知和心理功能。模块之间的自治性也对网络的鲁棒性产生了影响。假设大脑以某种方式受损，例如由于中风、创伤性脑损伤或深部脑刺激电极造成的损伤。在一个模块化的大脑中，这种损伤的影响仅限于起源于该模块的部分，只影响该模块支持的功能集合，但在更广泛的认知功能方面仍能保持不变。此外，模块化结构缓冲了隐性变异，使大脑更具进化性，从而提高适应性。它有助于降低布线总成本，支持丰富的动力学，并降低了布线成本。

有没有任何实证证据支持大脑具有模块化的假设？越来越多的研究已经使用聚类和社区检测算法揭示了现实世界结构和功能大脑网络的模块化结构。在这些研究中，大脑表现出模块化结构的最有力证据来自对静息态功能成像数据的分析。在这些研究中，从静息态获得的fMRI数据估计了功能连接性，并进行了聚类 - 在第一项研究中，将Infomap聚类算法应用于阈值化连接矩阵；在第二项研究中，将修改过的k-均值算法应用于完全加权且带符号的功能连接性。如预期的那样，这些算法将大脑的某些部分划分为模块。然而，聚类算法可能会误导，因为它们可以在没有真实聚类结构的网络中检测到聚类。为了缓解这个问题，两项研究都通过比较聚类的空间范围与前一项研究中的任务激活剖面进行了交叉验证。令人惊讶的是，静息状态下模块的边界限定了激活模式，这表明大脑的模块化结构支撑着支持积极认知处理的相同系统。

在另一项精妙的研究中，Crossley等人直接比较了静息态连通性的社区结构与任务共激活模式。使用来自BrainMap的数据，这是一个汇总和报告许多研究中的激活位置的数据库，Crossley构建了一个共激活矩阵，其中如果节点在类似条件下激活，则它们相互连接。作者随后将社区检测方法应用于这两个矩阵，并发现结果模块之间存在密切的对应关系。这些观察结果进一步表明，大脑内在的模块化结构描绘了其功能系统。

虽然已经就社区与大脑内在功能结构之间的对应达成一致，但仍存在许多悬而未决的问题。例如，社区的“真实”数量是多少？社区与功能领域之间是否存在一一对应关系？所有大脑区域都形成模块吗？所有模块都是隔离和同质的吗？

解决这些问题仍然是一个活跃的研究领域，并且在某些情况下需要方法论创新。以关于模块的“真实”数量及其各自大小的问题为例。许多研究报告称，大脑的模块化结构是分层的，较小的社区嵌套在较大的社区内。即使是实证研究也报告了大脑被划分为大大小小各不相同的簇，从大型任务正负二分法到这些系统的许多细分。然而，Infomap和模块最大化等方法将网络划分为单一尺度的模块和固定的社区集合。我们如何解决这一现实与预期模块应呈分层的矛盾呢？一个策略是采用多尺度社区检测方法。Infomap和模块最大化都包括可调节的自由参数，可用于检测不同大小和数量的社区，从而有效地描述了一个网络的社区结构，而不是优先考虑单一尺度。相反，它包含了大脑固有的多尺度和分层组织。

社区层面对功能和结构大脑网络的分析代表了一个活跃的研究和方法发展领域。像多层模块最大化这样的新技术使得可以同时对来自多个个体的数据网络进行聚类，以及成像模态和不同时间点。还有其他方法甚至挑战了大脑社区结构是模块化的基本假设。随机块模型对社区的特征做出较少的假设（Infomap和模块最大化都只能检测到同质性的网络神经科学和连接组学社区），如果核心-外围或非同质性社区存在，它们有能力检测到它们。一些最近使用块模型的研究发现了非同质性社区，这些研究表明，将这些特征纳入模型可以加强结构-功能关系，并与使用模块最大化估计的基因共表达模式更紧密地对齐。

中尺度分析还被用来表征个体差异，包括认知、临床状况以及跟踪大脑网络结构的发育和整个生命周期的变化。例如，越来越多的研究将模块的质量（用模块化函数量化）与行为、人口统计和认知变量联系起来，例如生物年龄、在认知要求较高的任务上的表现等。其他研究则将模块化作为预后指标，例如用来预测治疗和有针对性干预的结果。

其他研究则探讨了在进行认知要求较高的任务时，大脑的模块结构如何重新配置。汇聚的证据表明，任务激发模块结构的一个关键组织原则是，与静息状态相比，模块表现出增加的整合和减少的分离。也就是说，认知要求较高的任务似乎需要大脑模块相互协调，形成强大的跨模块链接。像随机块模型这样的方法报告了一致的发现，即在静息状态下具有同质性和分离性的模块被非同质性结构（如核心-外围结构）所取代，在某些情况下，这种结构是任务特异性的。

总之，从网络科学和连接组学的角度研究大脑的系统层面组织已经为神经科学的多个领域提供了信息，从理论到应用。这个课题仍然是一个富有成果的研究领域，并促进了方法的发展，并在所有空间尺度上有效地应用于大脑数据。

结构活动和连接性的基础

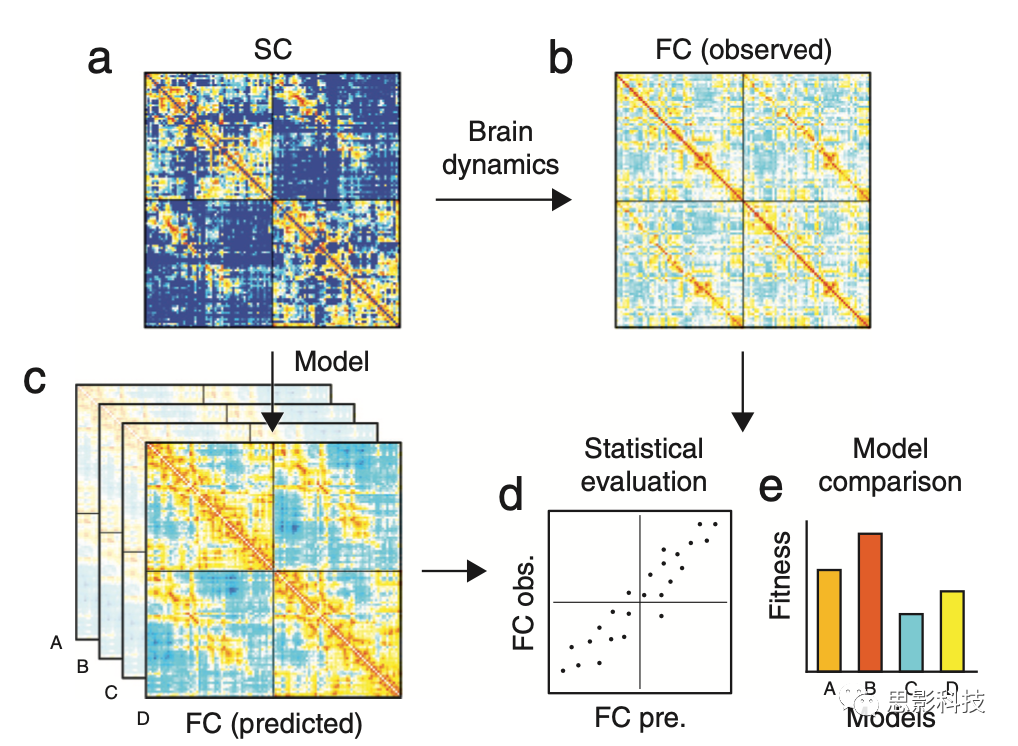
图 2.2 受结构约束的FC模型。结构连接（a）约束大脑动力学，从而导致相关的大脑活动，这些活动被测量为FC（b）。为了更好地理解这种结构-功能关系，可以构建大脑动力学模型，作为输出产生合成的FC模式（c）。这个框架使得可以测试不同的模型，这些模型对应于关于大脑动力学/通信的不同假设，具有不同程度的复杂性和生物物理合理性（d）。模型性能可以量化为观察到的FC和预测FC之间的相关性（e）。模型之间可以根据它们的性能作为适应度衡量进行比较，以识别最优的动力学模型。生物学中的一个核心问题涉及生物体结构与其能够执行的功能之间的关系。在网络神经科学的背景下，我们可以问一个类似的问题——大脑的解剖结构如何塑造大脑远离部位之间的功能耦合模式？直观地说，我们认为解剖连接是一组约束条件——大脑的某些部位通过白质或轴突投射直接耦合在一起，而其他部位则没有。那些连接在一起的部位可以方便地互换信息或相互发信号——而那些缺乏直接连接的部位只能通过多步路径间接交流，从而塑造大脑活动的相关结构。这种功能与基础解剖结构的耦合是大脑网络的一个基本特征，当其被破坏或扰乱时，可能导致不适应行为和疾病。结构功能耦合的破坏可能正是我们应该通过深部脑刺激（参见第1章）来调整的目标。

实际上，有大量实证和计算机模拟的证据表明，大脑结构连接性与功能耦合模式之间存在因果关系。一些最有力的证据来自损伤研究，其中直接的结构损伤导致功能连接的急性变化。奥赖利等人的一项研究是最清楚的例子，在这项研究中，在猕猴左右半球之间的胼胝纤维被手术切除之前和之后，估计了静息状态的功能连接。这种急性影响减少了大脑半球间功能连接的幅度，这可能是因为这些区域无法再相互交换信息或同步活动。

其他关于结构连接塑造功能耦合的证据来自计算机模拟研究，其中结构连接被视为网络动力学系统的一部分。这些概念如何应用于深部脑刺激领域。动力学系统的元素——网络中的节点——具有代表其活动水平的内部状态，例如，膜电位或BOLD振幅，并且可以根据一定的内部动力学随时间自由演化。当这些元素彼此耦合——即作为网络的一部分——那么每个元素状态的演化就取决于其邻居的状态。因此，结构连接施加的约束在时间上诱导了节点状态变化的相关性，从而导致观察到的功能连接模式（如图2.2b）。

这类模型通常包括生物物理参数，例如，“神经质量模型”包括兴奋性和抑制性神经元群，通道传导率，信号的时间滞后传播等。虽然这些参数的引入有助于保持一定的神经生物学可信度，但代价也是显而易见的。首先，求解微分方程组在计算上是昂贵的，即使在高性能计算机上运行几个小时也只能产生几分钟的数据（尽管新的软件包承诺减少运行时间）。其次，合成时间序列的相关结构与其经验对应物之间只有适度相似，这表明生物物理模型可能缺少关键组件或参数。这种较高的计算成本和较低的解释方差促使人们探索基于解析易处理、风格化的动力学的更简单和更容易解释的模型，这些动力学代表大脑区域间相互沟通的假设策略。

与生物物理模型不同，输出是合成时间序列，通信模型为所有区域对生成通信容量或两个大脑区域相互沟通的容易程度的度量，从而产生一个方形的节点矩阵。例如，假设我们假设大脑区域通过网络的最短路径结构传递信号进行“沟通”。作为这个假设的粗略测试，我们可以计算所有大脑区域对之间的最短路径长度，并将结果的最短路径矩阵的元素与经验功能连接矩阵的元素进行比较。通常情况下，两个矩阵之间更强的对应关系可以被解释为支持最短路径对大脑通信重要的证据。

为了利用最短路径进行信号传输，这些“信号”需要具有整个网络及其最短路径结构的全局知识。在另一个极端是分布式过程，如扩散模型，其中粒子或随机游走者（代表一些信息量）在网络上随机移动，无偏地从一个节点跳到另一个节点。从这个过程中，可以计算出诸如平均首次通过时间这样的度量，即一个粒子从一个节点开始预期到达另一个节点所需的时间，并将这些度量与功能连接进行比较。其他简单的模型包括基于可通性的模型，其中节点沿着所有路径进行通信，但指数级地减少较长路径，振荡器模型，其中节点根据邻居的相位更新自己的相位，以及基于隐藏度（随机游走者无误差地沿最短路径行走所需的信息量）的节点间路径进行量化的搜索信息模型。

这些简单的模型使研究人员得以探索和比较各种可能的通信策略，从多路径通信到为脑成像数据改进的传播模型，再到分布式和贪婪的导航模型，以及基于信息的模型。由于这些模型基于解析易处理的度量，它们具有较低的计算成本，可以轻松实现并优化其参数。关键的是，这些模型在预测经验功能连接方面往往优于更具神经生物学合理性的模型（见图2.2d和e）。

总的来说，有大量的实证和计算机模拟证据表明，结构连接在塑造功能耦合模式方面起到了因果作用。这些证据促使许多研究考虑正常结构-功能耦合受到干扰的情况，例如在任务执行过程中，神经精神疾病中，或者在人类发展过程中。实际上，结构-功能耦合的变化与任务表现、受试者人口统计特征和特质之间的个体差异存在关联。

然而，仍有许多悬而未决的问题和挑战。例如，结构连接和功能连接之间的测量关联可能取决于其他因素，包括大脑的空间嵌入——两个区域之间距离越近，它们通过两种模态相互连接的可能性就越大。这种相互依赖于距离使得评估结构-功能耦合的真实强度变得困难。其他挑战更为根本。结构连接和功能连接矩阵的准确性在大多数分析中仍是一个令人担忧的问题。特别是结构连接，它存在已知的偏见，阻止了对某些白质束的准确推断。功能连接也存在一系列特殊的偏见，包括归因于扫描仪中头部运动的变化。更根本的是，功能耦合的事实上的度量——皮尔逊相关——代表了许多可能的连接度量之一，结构-功能关系的强度通常会随着这些度量而变化。

如果您对脑网络数据分析感兴趣，可浏览思影科技课程及服务，另思影可承接PET相关数据处理分析业务，感谢转发支持（可添加微信号siyingyxf或18983979082咨询，另思影提供免费文献下载服务，如需要也可添加此微信号入群）:

重庆：

第三十一届扩散成像数据处理班(重庆，4.7-12）

第七十九届磁共振脑影像基础班(重庆，4.14-19）

第九届影像组学班（重庆，5.20-25）

第八十三届磁共振脑影像基础班(重庆，6.9-14）

上海：

第七届扩散磁共振成像提高班（上海，4.14-19）

第八十一届磁共振脑影像基础班（上海，5.6-11）

第二十八届脑影像机器学习班（上海，5.14-19）

第二十五届磁共振脑影像结构班（上海，5.23-28）

北京：
第八十届磁共振脑影像基础班（北京，4.19-24）
第二十七届脑影像机器学习班（北京，5.5-10）
第十三届任务态功能磁共振数据处理班(北京，5.24-29）

第十届影像组学班(北京，6.11-16）

第三十九届磁共振脑网络数据处理班（北京，6.20-25）

动态连接组学

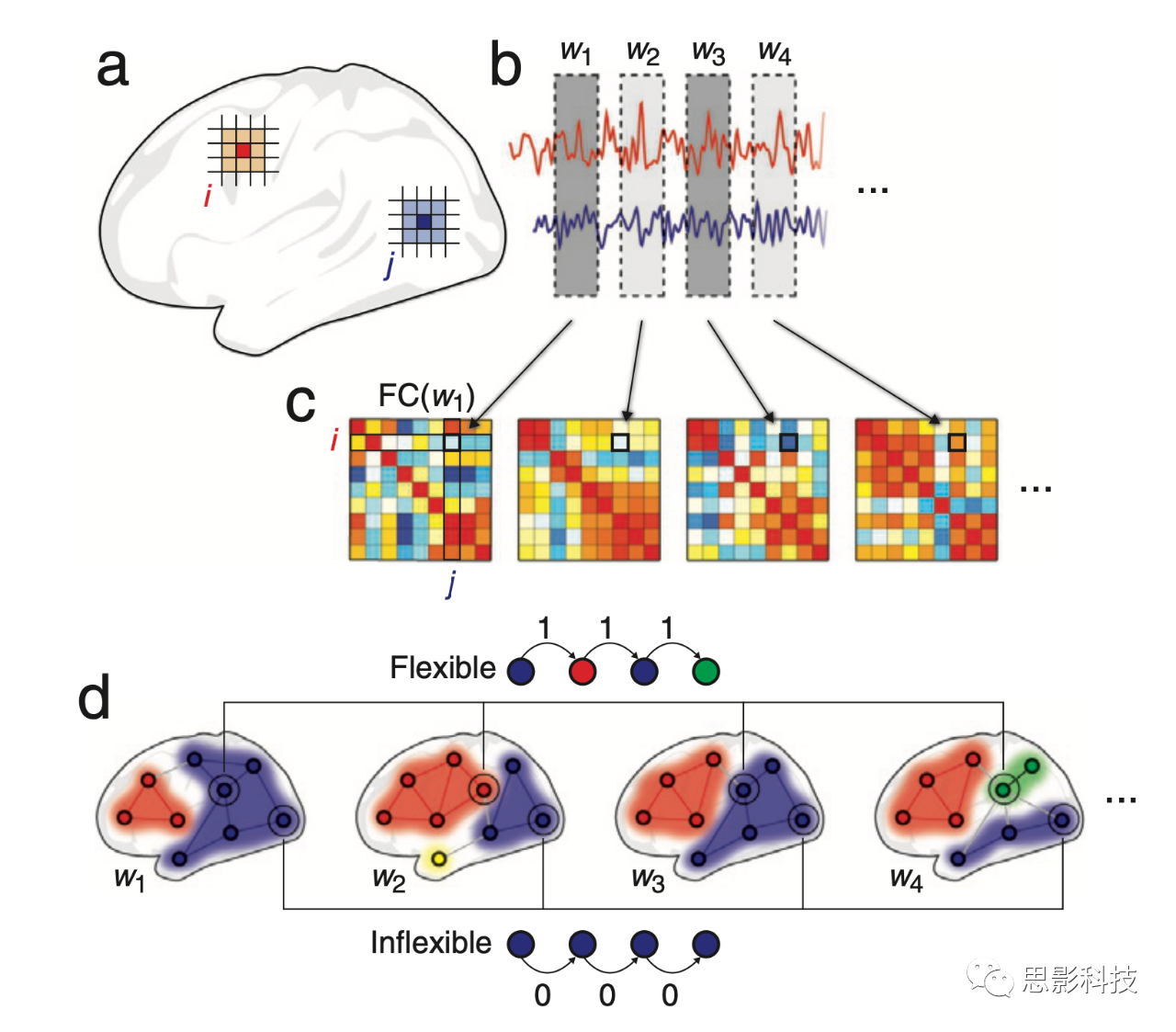
图 2.3 时变FC和灵活性。为了研究网络组织随时间的变化，滑动窗口方法通常用于获得时变FC的估计值。

(a) 这涉及从大脑不同部位提取时间序列。

(b) 然后对时间序列进行“窗口化”，并仅使用落在给定窗口内的点来估计FC权重。对于一对体素/顶点/区域，这导致一系列与该窗口时间局部化的FC估计值。

(d) 尽管时变FC可以使用许多不同的方法进行分析，但一种常见的方法是基于网络模块的重构来估计网络灵活性。这个过程涉及从时变矩阵构建一个“多层网络”，并同时对所有时间点进行聚类。灵活性计算为节点从一个时间点到下一个时间点改变其模块隶属关系的频率。这里，我们展示了一个灵活的节点（顶部）和一个不灵活的节点（底部）的示例。

连接组学革命带来的一个深刻认识是，即使在认知休息期间，大脑也从未安静下来。相反，人类大脑始终在不断变化，随着时间推移，穿越一个高维度的活动和连接模式的景观。特别是随时间变化的功能连接（FC），引起了网络神经科学领域的极大关注。在这里，人们普遍认为，随着时间的推移，神经元素之间的瞬时耦合和解耦反映了认知状态的变化，通过研究这些变化，我们可以洞察到功能网络在快速时间尺度上支持心理过程的原理。 许多方法已经被提出来研究动态或时变功能连接，包括基于频率的分解、瞬时共波动分析和基于模型的方法。然而，最常见的方法是滑动窗口方法。这需要指定一个包含临时连续时间点的某种长度的“窗口”（图 2.3a 和 b）。然后，使用给定窗口内的时间点计算时间分辨功能连接，并将窗口向前推进固定数量的时间点，然后重复该过程。结果是一系列对应于不同时间点的功能连接模式的网络（图 2.3c）。然后可以分析这些网络以了解网络动态——大脑在时间上的拓扑组织如何波动。

尽管可以使用许多不同的方法分析随时间变化的功能连接（FC），以量化跨时间的模式稳定性和可变性，但一种流行的研究方法是根据相似的FC模式将时间点分配给聚类。这个过程产生了一组脑状态——簇质心——描述了大脑随时间穿越的低维空间。这些状态可以使用丰富的统计数据进行总结，包括每个状态的相对频率和从一个状态转换到另一个状态的概率。这种方法已被广泛使用，并已成功将随时间变化的连接性与唤醒和清醒、注意力、意识状态等联系起来，并已在临床环境中应用，以生成疾病和神经精神疾病的生物标志物。

研究时变连接的另一种强大方法是使用多层网络模型跟踪不同时间的社区变化（图 2.3d）。在这种方法中，不同时间点的FC模式被视为单个多层网络中的“层”，其中每个层与其时间相邻的邻居层弱耦合。当多层网络被聚类时，所有层同时被聚类，其聚类标签得以保留。这使得可以直接比较在时间相邻层的节点聚类标签，以识别频繁切换聚类分配的灵活节点和那些在时间上保持稳定分配的节点。这种方法可用于跟踪随时间形成、持续和消失的社区。灵活性可以在整个大脑和局部区域计算，在以前的研究中被证明是认知和疾病的有力生物标志物。越来越多的研究将灵活性模式与学习、执行功能、情绪和情感状态以及工作记忆联系起来。其他研究将灵活性与精神疾病和精神分裂症联系起来。

虽然使用滑动窗口方法分析时变功能连接（FC）非常普遍，但这个过程要求用户在其中做出一些非琐碎的处理决策。这些决策包括确定窗口长度以及是否应该进行锥形减少，以及每一步窗口应该推进多远。尽管改变长度是研究不同时间尺度的网络变化的简单方法，但窗口长度也会影响抽样可变性。这导致了时间尺度与误差之间的权衡，其中较短的窗口可以揭示FC中较快的时变变化，但假阳性和假阴性的比例较大。

还有一些问题挑战了使用fMRI方法测量时变FC的概念。这些研究认为，由于fMRI采用的测量方法缓慢且间接，时变FC分析中观察到的可变性与来自时间上稳定且不变的相关结构的抽样可变性一致。这种观察要求将时变连接性的任何估计与稳定的零模型进行比较。

总之，时变网络分析正在广泛应用于研究较短时间尺度上的网络结构变化。这些分析的结果为大脑网络随时间重新配置的原理提供了深入了解。虽然这个领域的研究有时存在争议，但它继续加强了网络拓扑结构的快速变化与认知状态波动之间的联系。

未来有什么展望？

像任何年轻的领域一样，连接组学和网络神经科学的全部潜力尚未被挖掘，许多前沿领域都在进行令人兴奋的新工作。在这一部分，我们回顾了其中的几个领域，重点关注生成建模、网络控制和基于边的方法。

生成建模

图 2.4 连接组模型的生成模型。

网络生成模型旨在揭示产生观察到的大脑网络（A）的连线规则。 (B) 通过提出和测试不同的模型——生成过程——并评估它们与观察到的网络特征的匹配程度来实现这一点。生成过程可以是简化的、在非生物时间尺度上进行的，也可以包含详细的神经生理细节并在发育时间上进行。 (C) 这个过程通过状态空间追踪轨迹，其中生成的大脑网络作为结果，用某种距离/相似度度量与观察到的网络进行比较（D）。生成建模框架允许进行计算机内探究干预。例如，如果两个网络沿着类似的轨迹演化——一个朝着有利的健康状态，另一个朝着不利的疾病状态——可以通过探索不利轨迹的有针对性的干扰来识别将大脑“驱使”回到健康状态的策略（E）。可以实例化测试网络增长和演化的不同假设的不同生成模型，并将它们的适应性（与观察到的网络特征的匹配程度）进行比较，以了解塑造大脑网络组织的连线规则和原则。

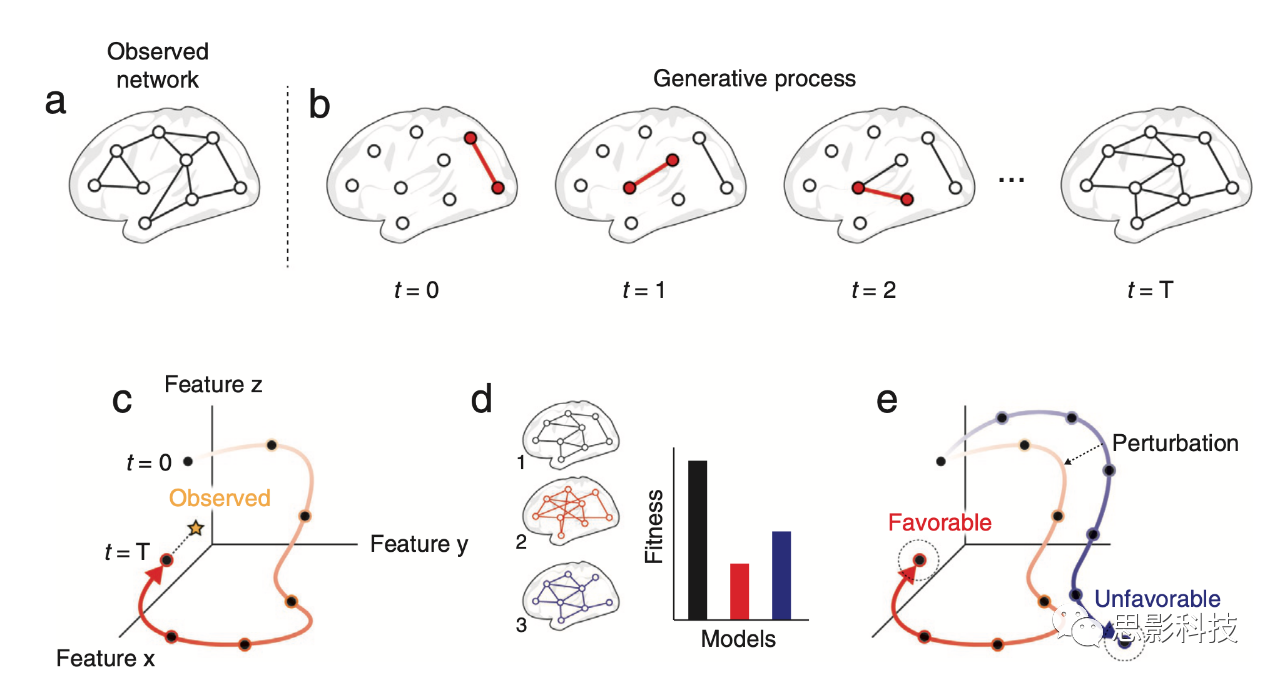
网络神经科学的吸引力部分在于使用不断增长的概要统计工具套件来量化大脑组织的不同方面的能力。正如前面所提到的，这些测量可以诊断有影响力的节点，发现社区，并评估网络进行有效信息传输的能力。然而，网络概要统计只是描述和总结网络。也就是说，概要统计并不能解释为什么网络具有某种特征，或者这种特征是如何首次出现的。要了解网络增长和演化的过程、规则和算法，需要构建、测试和验证生成模型。

生成建模在网络科学中有着丰富的历史，以Watts-Strogatz和Barabasi-Albert模型为基础，最为典型。虽然这些模型提出了小世界性和集线器产生的机制，但一般来说，生成模型的工作原理是确定网络需要具备的一组期望特性，并向后寻找产生具有这些特性的网络的过程。

与其他建模练习一样，简约在生成建模中发挥着重要作用，生成建模研究通常旨在发现能够准确复制真实大脑网络属性的“简单”连接规则。然后，这些规则可以被解释为大脑网络组织的驱动因素。任何由于这些规则而偶然产生并作为这些生成机制的有用副产品的其他特征都可以被认为是“拱券”。（注释：在生物学领域，拱券是一个指代那些原本不是由自然选择直接产生的特征，而是作为其他自然选择过程中适应性特征产生的副产品的概念。）

大脑网络可能的生成模型空间是巨大的。我们可以通过按照它们如何处理时间对模型进行分类来为这个空间施加一些秩序。在一个极端，有些模型是在生物学有意义的时间尺度上使网络生长和演化的，目的是重现特定的发育轨迹。这类模型需要根据观察仔细校准，并包括其他神经生物学细节，然后可以用来评估扰动如何改变发育轨迹（导致适应不良的大脑网络），并探索在将大脑恢复到健康轨迹的策略。尼科西亚等人的研究是这类模型的一个很好的例子，他们模拟了线虫（秀丽隐杆线虫）的生长。我们拥有关于C. elegans大约300个神经元出生时间的详细信息，这些信息可以纳入生成生长模型，以重现成年C. elegans的网络。作者证明了一个基于出生时间结合惩罚形成长连接和奖励高度节点的布线规则的模型可以解释成年C. elegans连接组的许多特性，包括双相生长速率。

在另一个极端，有些模型中时间不起作用，如随机块模型，或以非生物学方式处理时间。Barabasi-Albert模型就是一个很好的例子，网络根据一组简单的规则生长，随着时间的推移添加节点和边缘，但时间尺度是任意的。虽然这些类型的模型缺乏生物现实主义，但它们可以用来深入了解塑造网络组织的基本原则。例如，最近的一些网络神经科学研究调查了准动态模型，这些模型根据概率生长规则逐渐向一组大脑区域添加边缘。在这些研究中，作者基于网络的空间布局和拓扑结构测试了许多可能的规则，比较了它们解释实证大脑网络的组织特性的能力。在这两种情况下，作者发现最优模型—生成与现实世界大脑网络相似特性的合成网络—惩罚形成长距离连接，但增加了具有相似连接特征的节点之间形成连接的可能性。尽管这些模型的时间尺度与神经发育没有任何对应关系，但它们的结果与C. elegans的生成模型是一致的。

生成模型在揭示大脑网络组织原理方面发挥了重要作用。其中一个关键发现是空间关系在塑造大脑网络结构中所起的作用。大脑必须被限制在有限的体积内，它们的连接需要物质来形成并且需要能量来维持和使用。因此，较短的连接可以减少体积和布线成本，并提高适应性。尽管有些研究认为降低这些成本足以完全解释大脑网络组织，但大多数研究认为，这种驱动力需要被一些相反的力量来平衡，以解释涉及长距离连接的大脑网络的昂贵特性，例如，枢纽和富集俱乐部的存在。

生成模型方法为研究大脑网络及其在健康和疾病中的作用提供了新的、令人兴奋的策略。首先，生成模型有助于发现网络组织的驱动因素，从而将注意力重新集中在这些特征上，远离“拱券”，这有助于生成越来越敏感和适当的生物标志物。其次，生成模型可以适应特定主题的数据，其参数可用于研究个体差异。例如，在某文献中，作者证明了控制空间约束的参数随年龄而变化，而作者在另一篇文献中使用了类似的模型，并证明了它们的参数与精神分裂症的多基因风险和认知表现相关。最后，通过将额外的神经生物学和发育细节纳入它们的布线规则，生成模型可以为人类发育提供深入的见解。

网络控制

为了满足持续的认知需求，人类大脑必须有序地从一个大脑状态无缝地过渡到另一个状态。大脑是如何实现这一点的？这些转换是如何得到基础解剖连接的支持的？这类问题可以用网络控制框架来解决。这种方法预先设定大脑是一个网络动力学系统，假设在没有任何干预的情况下，每个大脑区域的活动会根据自身状态和连接邻居的状态随时间演变，随时间描绘出一条轨迹。然而，这条轨迹可以通过外源性时变输入信号被“注入”到大脑区域中来改变。因此，这些信号可以驱动大脑活动，使其偏离其被动轨迹。网络控制理论提出了这样一个问题，即是否有可能定制这些输入信号，以便大脑不是简单地沿着不同的轨迹运行，而是沿着特定的预定义轨迹运行，同时使用尽可能低幅度的控制信号。

通过这种方式，网络控制提供了一个优雅且数学上可处理的框架，自然地将大脑连接性、动力学和活动联系起来。一方面，它可以产生一组局部和全局的网络度量。这些包括大脑区域的控制特征-它们将大脑驱动到某些类别的大脑状态的能力，例如，那些难以达到并需要付出大量努力才能达到的状态，相对那些容易达到、需要很少努力的状态。我们还可以计算出全局度量，揭示网络是否可控，即其拓扑结构和动力学是否允许其被驱动到任意状态。像其他网络度量一样，控制指标可以为个体计算，并用于研究个体间或群体间差异，并已被用于揭示发展过程中的变化、控制和临床人群之间的差异，以及了解创造力的结构和动力学基础。

实际上，大多数大脑状态从未被访问过。也就是说，它们对应于代表非功能性“噪音”的活动模式，或者访问它们具有主动危险性，例如癫痫发作或癫痫活动。为了使控制措施更具信息性和现实性，我们应该专注于主动访问的大脑状态之间的过渡，忽略那些由于某种原因而未被访问的状态。实现这一点的方法之一是利用最优控制框架。最优控制框架不考虑从所有可能状态到达和离开的过渡，而是考虑特定状态对之间的过渡：系统开始的初始状态和试图达到的目标状态。给定一组控制节点，通过这些节点注入输入信号，最优控制提供使大脑从初始状态到达目标状态所需的尽可能少的努力的时变输入。控制能量的数量取决于初始和目标状态的特性，还取决于底层结构网络的拓扑结构。最优控制框架产生一系列可在个体之间或不同群体之间进行比较的统计数据。这些包括节点轨迹、输入信号和支持过渡所需的控制能量。这些度量已经在几个应用背景中得到应用。例如，Cornblath等人计算了大脑活动模式的聚类作为大脑状态，并证明最频繁的状态过渡需要最少的能量，这表明大脑的白质网络支持其通过状态空间的动态轨迹。同样，Braun等人计算了在工作记忆任务期间从活动状态过渡到和离开所需的能量，并将能量量与多巴胺受体表达联系起来。

一方面，网络控制的前提——我们可以选择性地驱动大脑进入具有不同认知和行为类似物的不同活动模式——看起来像是科幻小说。然而，网络控制理论在现实世界中具有实际应用和实际意义。例如，随着植入式神经调控设备的出现，非侵入性刺激（如经颅磁刺激）的广泛使用以及光遗传控制群体级活动的实践，新理论有必要对目标刺激的影响进行建模和预测。然而，使用网络控制仍存在一些实际障碍。迄今为止，大多数将网络控制应用于大规模大脑网络的研究都假设大脑活动是由线性动力学描述的。虽然这个假设有助于简化控制的数学方法，但控制非线性动力学比线性控制要困难得多。另一个问题涉及可控性度量与更容易获得的传统网络度量之间的关系，例如节点度。有几篇文章表明，这些度量高度共线，暗示决定节点控制特性的不是网络的拓扑结构，而是节点的低级特征，例如它们建立的连接数。这意味着真实和随机网络的控制特性几乎相同。

尽管如此，网络控制在连通组学中代表了一个激动人心的新领域。它揭示了一种令人着迷的可能性，即利用对底层结构连接的了解来选择性地驱动整个大脑活动模式。虽然这个框架主要局限于理论练习，但新的操纵大脑活动的方法（包括深度脑刺激）将提供可以仔细测试和进一步完善理论的案例。

边-中心网络

图 2.5 神经影像数据的边为中心的建模和分析。边为中心的模型将焦点从单个大脑区域及其活动转移到区域对及其共同活动。(a) 首先提取并对区域/分区时间序列进行 z 标准化，这恰好是计算 fFC 的前两个步骤。(b) 对于每一对时间序列，我们计算它们活动的逐元素乘积，得到一个共同活动或共同波动时间序列。(c) 为所有大脑区域对执行此过程，产生一个“边”时间序列矩阵。(d) 边时间序列矩阵的每一列代表在特定时刻表达的共同活动模式。这些模式可以重塑为一个区域对区域矩阵，并作为一个功能网络进行分析。(e) 边时间序列还可以用来创建一种新型的连通性矩阵：“边功能连接性”(eFC)。这是通过计算所有可能的边时间序列对之间的两两相似性来实现的。与节点 FC 不同，后者产生一个区域对区域矩阵，而 eFC 矩阵具有节点对乘以节点对的尺寸，即边乘以边。这个矩阵可以进一步分析，例如，聚类以揭示重叠的社区。

历史上，大脑网络通常使用“节点中心”的网络进行建模和分析，其中节点和边代表神经元、种群或区域，以及功能或结构连接。这种模型一直是网络神经科学的基石，几乎是迄今为止所有连通组学发现的核心。然而，最近，一些团队提出扩展节点中心模型，以表征网络中的高阶相互作用。这意味着将关注点从大脑区域和神经元素之间的相互作用转移到功能和结构连接之间的相互作用，并构建全新的网络类别。

生成高阶“边中心”网络的两种最常讨论的方法包括将传统的节点对节点连接矩阵转换为更高维度的边对边“线图”和“边相似性”矩阵，这些矩阵量化网络中边对的相互作用强度。虽然这些方法在其他学科中已经成功应用，但在神经科学中的应用却受到了限制。迄今为止，只有一项研究将边缘中心方法应用于实证大脑网络，使用线图研究结构连接数据的重叠社区结构。

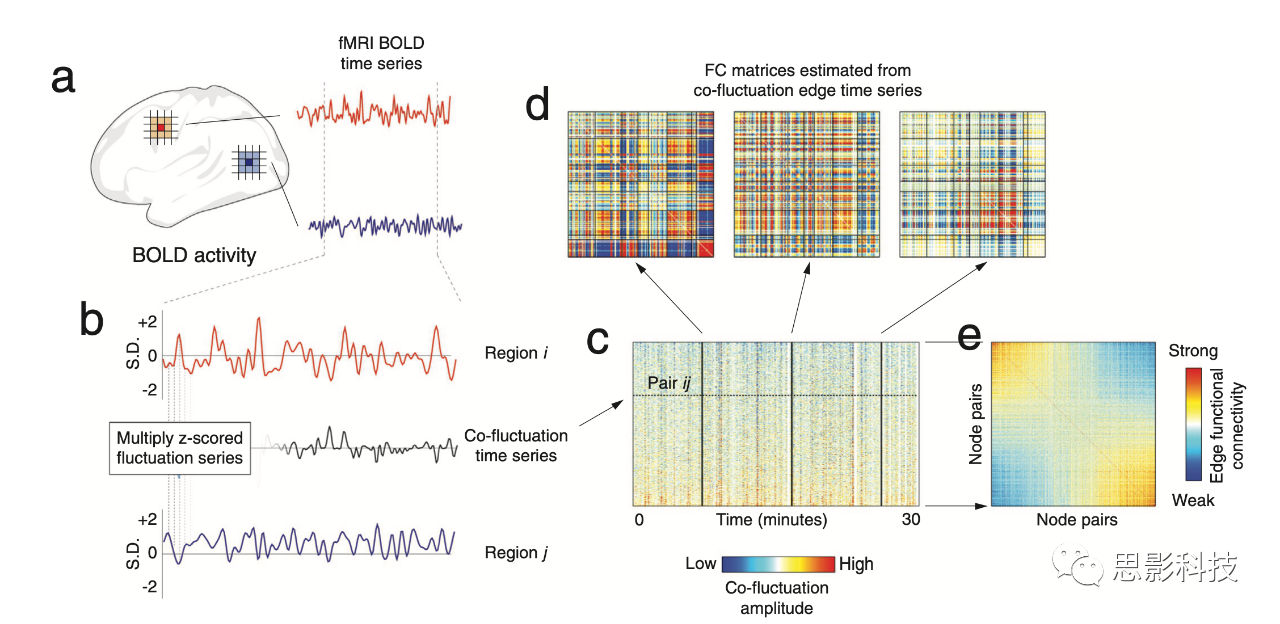
然而，最近几篇论文提出了一种新的生成高阶网络的方法，使它们更容易应用于神经影像数据，并为研究大脑的高阶组织和动力学开辟了新的机会。这种新的边中心模型基于时间序列和双变量皮尔逊相关性——这是定量功能连接的常用度量。虽然两个区域的活动的皮尔逊相关性是通过计算它们的标准化（z-分数）时间序列的平均逐元素乘积来计算的，但边中心模型省略了平均步骤，为每对节点（边）生成一个共波动时间序列。因为功能连接通常被解释为两个大脑区域之间通信的指标，我们可以将每个边时间序列看作是该“对话”的时间解析记录。

该过程可以针对每一对大脑区域（网络中的所有边）进行，生成一整套共波动时间序列（也称为“边时间序列”），具有有用的特性。首先，我们可以将边时间序列视为功能连接的时间分解；任何一对节点的共波动时间序列的时间平均值正好是这些节点之间功能连接的权重。有了这种分解，我们可以评估单个帧对平均功能连接的贡献。此外，如果我们在某个时间点“切片”边时间序列，我们将获得所有边对的瞬时共波动模式，可以将其重新整形为一个区域与区域的矩阵并作为网络进行分析。因此，边时间序列在不使用滑动窗口的情况下量化网络结构的时变变化，从而提高了时间分辨率。

有趣的是，边时间序列呈现出突发性，也就是说，在大多数时间点上，幅度较弱，但在非常短的时间内变得极强。更有趣的是，这些突发发生的时间往往在各个边之间呈现相关性，导致时变网络中大多数连接较弱，但偶尔会被罕见且短暂的高幅度“事件”所打断。尽管事件发生的频率较低，但它们在静态功能连接中解释了不成比例的方差，解释了其系统级结构，并包含了不在低幅度帧中出现的特定于受试者的信息。

边时间序列还可以用于估计更高阶的边功能连接性（eFC）结构。通过计算边时间序列对之间的相似性，可以得到类似于线图和连接相似性网络的边与边连接矩阵，但它是完全加权且带符号的。像传统的节点为中心的网络一样，可以使用网络科学工具分析eFC，以识别网络中重要或有影响力的边。然而，eFC的主要优势在于使用社区检测算法将边划分为紧密波动的边时间序列社区。在这种情境下，边被分配到单个社区，但由于每个节点与许多边相关联，每个边都可以属于不同的社区，网络中的节点可以具有多个社区隶属关系。与其他解决重叠社区的方法不同，在这些方法中，少量节点在多个社区中弱参与，边社区导致“普遍重叠”，使得节点被多个重叠社区覆盖。这种普遍重叠的概念符合我们对大脑功能的理解；即使是传统的“单模态”大脑区域也对各种不同的刺激和条件作出反应。

在Faskowitz等人的一项研究中，使用熵度量来量化每个大脑区域的重叠程度，揭示出异质性模式。有趣的是，观察到感觉运动和注意网络中的重叠程度最高，这表明这些区域可能在支持广泛认知功能方面发挥着以前未被揭示的作用。

总之，边为中心的方法为我们提供了另一个角度来研究大脑的组织、功能和动态。正如结构连接和功能连接提供互补的见解一样，边连接性也揭示了在快速时间尺度上共波动模式的变化，并描述了大脑的高阶相互作用。边为中心的方法为未来的研究提供了多种机会。首先，我们可以利用边时间序列将功能连接分解为其逐帧贡献的事实来重构功能连接，仅使用选定的帧子集。这些子集可以以特定的方式选择，以最大化重构的功能连接与行为之间的关系或增强组间差异。eFC本身似乎对放大网络中受试者特异性特征非常有用，这为增加个性化可能会改善个体差异研究提供了可能性。

结论

数据的可用性、分析框架和计算资源的完美结合为网络神经科学和连接组学的繁荣创造了有利条件。这些新兴学科为探索健康和疾病状态下的大脑连接模式以及在广泛的时空尺度上提供了量化框架。这个框架开始揭示大脑网络的一些关键特征 - 小世界结构用于高效信息处理，模块用于支持专门的信息处理，中枢和富俱乐部用于在模块之间整合信息，以及对空间布局的强烈依赖，有助于降低大脑的材料和代谢连接成本。连接组学的未来包括揭示网络层级机制和控制大脑活动的强大新方法，而新的记录和成像技术使得在越来越精细的空间尺度上解析网络成为可能，同时受益于更广泛的大脑覆盖。

网络神经科学和连接组学革命带来了许多先进的概念，这些概念在网络神经科学领域内不断被探索和改进，如时变连接性、网络控制和边为中心的连接组学在应用领域，如连接组学深脑刺激中具有潜力。因此，很可能在未来的研究中，这些和其他网络神经科学的前沿方法将从理论练习转向实际应用。

如需原文及补充材料请添加思影科技微信：siyingyxf或18983979082获取,如对思影课程及服务感兴趣也可加此微信号咨询。另思影提供免费文献下载服务，如需要也可添加此微信号入群，原文也会在群里发布，如果我们的解读对您的研究有帮助，请给个转发支持以及右下角点击一下在看，是对思影科技的支持，感谢！

微信扫码或者长按选择识别关注思影

非常感谢转发支持与推荐

欢迎浏览思影的数据处理业务及课程介绍。（请直接点击下文文字即可浏览思影科技所有的课程，欢迎添加微信号siyingyxf或18983979082进行咨询，所有课程均开放报名，报名后我们会第一时间联系，并保留已报名学员名额）：

核磁：