100多年前,Ramon y Cajal提出假设,在哺乳动物大脑连接的进化过程中,有两种力量在起作用:最大限度地降低连接成本和最大限度地提高传导速度。利用扩散张量MRI,本文作者重建了123种哺乳动物的大脑连接体。网络分析显示,哺乳动物的连通性和连接成本都是守恒的。作者的结果描述了保持大脑整体连接的守恒原则:半球间连接较少的物种表现出更好的半球内连接。
结果表明,有些物种的大脑半球间连接更多,半球内连接更少,反之亦然。同样的模式也适用于物种间,包括人类(人类的MSP与连合比例的斜率与所有哺乳动物没有区别)。本研究在探究哺乳类动物大脑的结构连接的连接成本和连接效率方面平衡方面存在跨物种和物种内部的一致性方面做出了巨大的贡献。
研究背景:
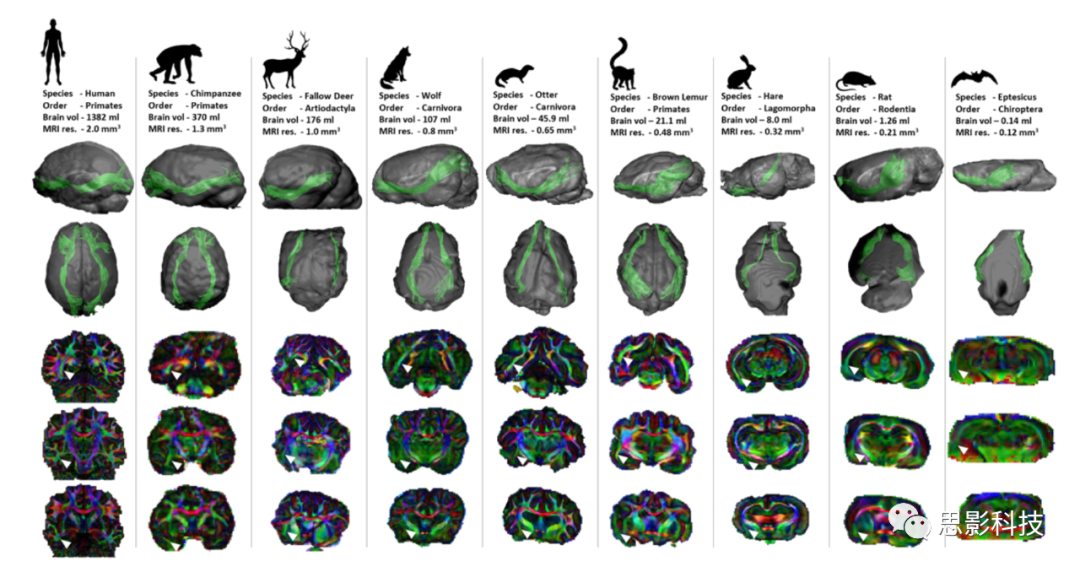
哺乳动物的大脑是物种进化过程中最复杂的生物系统之一。以前大多数对哺乳动物大脑的比较研究都集中在灰质,但是大脑连接体(即白质连接)的完整网络——对大脑功能的重要性与神经元一样,但只有少数研究使用物种间比较的方法考察了它的演化。本文利用扩散张量成像技术研究了123种哺乳动物的宏观白质连接,这123种哺乳动物来自12个不同的哺乳目种属(具体见图1a),这些动物的脑容量从小于0.1ml到大于1000ml都有。在所有物种中,都利用大脑体积对大脑体素的大小进行归一化,使得最终所有大脑获得的体素数量都差不多。
从以往研究的观点看,引导连接体进化的主要因素之一是快速信息传输和连接成本之间的权衡。一方面,为了更高的连通效率,需要更多更长的连接(为了能够形成小世界网络,不仅需要近距离节点间的连接,也需要大量远距离节点间的连接以能够更快的完成远距离通信),但另一方面,它们增加了连接成本(这主要是因为连接更长时,信息传输所需要的能量就更大,消耗会增加更多,提升通信成本)。为了验证这一点,本文首先使用网络的平均最短连接(Mean short path,MSP)量化了哺乳动物之间的连通性,这是一种衡量全脑网络通信的方法。MSP反映了网络的两个节点之间通信需要的最小步骤数(连接)。之所以采取MSP指标,是因为该指标与连通性成反比,即MSP越高,连通性越低。
尽管哺乳动物的大脑大小和形状存在巨大差异,但全脑连接性是如何保持的呢?哺乳动物的宏观连接体大致可分为两个半球网络,它们通过连合纤维相互连接,并通过半球内联合纤维相互连接。连合纤维的数量和排列在哺乳动物中差异很大。当观察到大脑之间的整体连接是恒定的(图1c和补充图2),作者假设,连接较少的大脑半球内网络必须以某种方式进行调整,以允许整体上相似的连接。需要注意的是,在这个部分的假设验证中,作者检查的是半球内的MSP,而不是之前图1中使用的全局MSP。重要的是,因为本次研究总是在所有物种中随机取样4000个半球连接(见方法),而且因为所有网络都有相同数量的节点(200),所以在半球内MSP中观察到的任何变化都应该反映半球连接的实际变化。
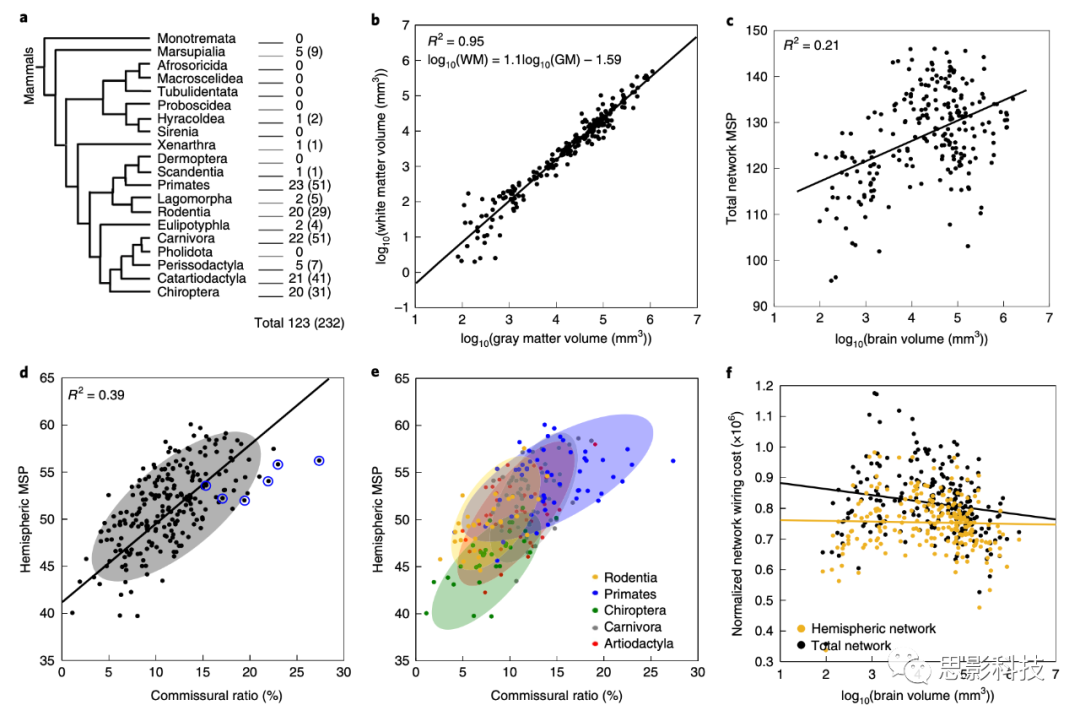
图1 跨物种哺乳动物的全脑连通性
注释:
图a:MaMI数据库包括123种物种的扫描结果。括号内的数字表示对一些物种的多个个体进行了扫描;
图b:在对数尺度上,白质(WM)体积与灰质体积呈线性相关,其斜率系数为~1.19 (P <10 -10,皮尔逊相关检验;n = 232)。
图c:全脑MSP与对数尺度的脑容量具有显著的相关(P <10 -6, Pearson s相关,n = 232)。MSP是在加权网络(以1/经过的纤维数目)上计算的,因此实际的MSP值是在议定标度上表示的。相关P值的报道没有进行系统发育校正。
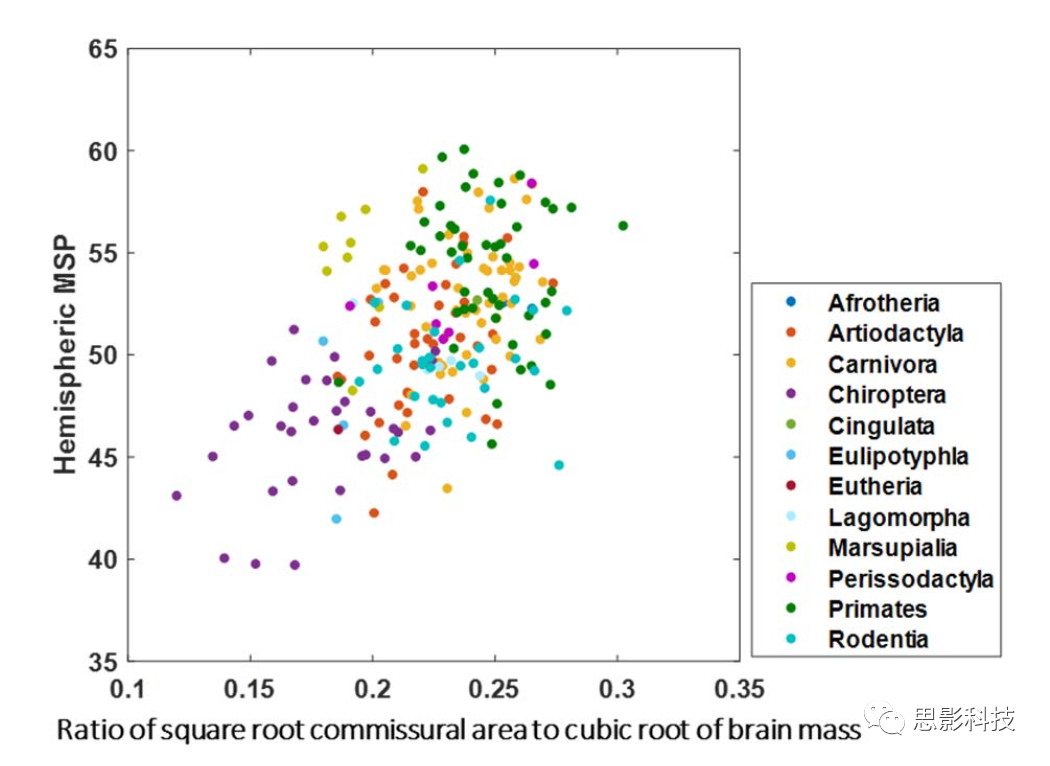
图d:所有哺乳动物的半球MSP与连合纤维的比例显著相关(n = 232)。六名人类被试被标上了蓝色的圆圈。图e的数据和d是一致的,但e标注了不同属目动物的颜色,可以看出同一属目的距离更近,带颜色的阴影部分是95%置信区间。
图f:半球(橙色)和全脑连接(黑色)成本与对数尺度的脑体积相关检验结果(Pearson s相关性,R2 = 0, P = 0.58, R2 = 0.03, P = 0.008,分别为半球和总网络;n = 232)。全脑连接成本的相关性是显著的,但可解释的方差变异是很小的。
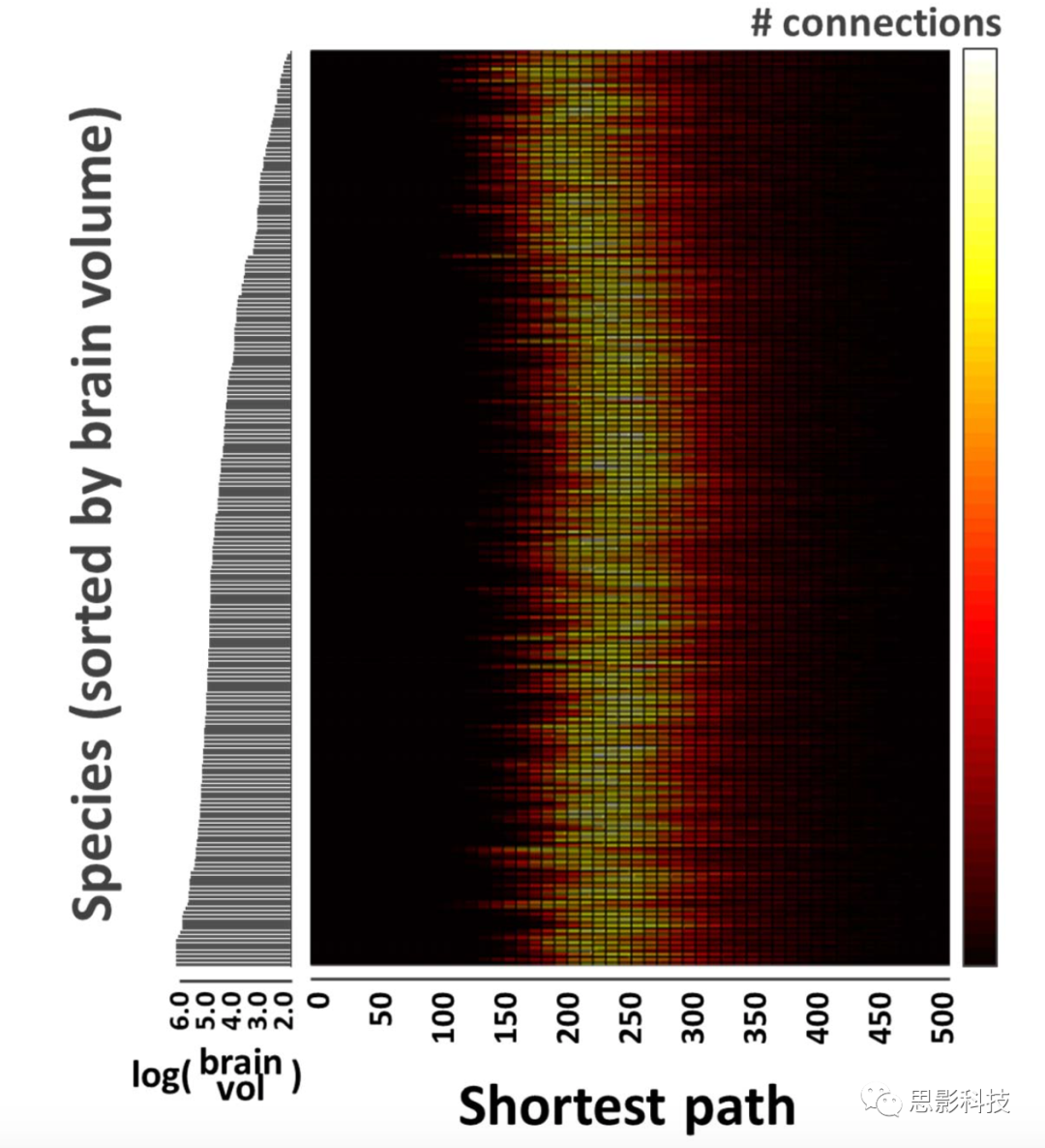
补充图2 在所有跨物种哺乳动物中网络连接最短路径的分布
注释:纵坐标是在对数尺度上按照大脑总体积大小排序的不同物种的脑容量,横坐标是全脑最短路径数目,color bar代表的是在该体积下,最短路径长度数目最常出现的比例,颜色越浅代表越典型。
研究方法:
样本:
哺乳动物MRI (MaMI)数据库包括123种不同物种的弥散扫描和T2-/t1加权扫描,其中一些物种的样本达到了232个大脑(补充表1)。本次研究获得了尽可能多的样本,远远超过以前的比较方法的研究。所有的扫描(除了人类参与者)都在切除和固定的组织上进行。扫描使用7-T 30/70 Biospec Avance Bruker系统或3-T西门子Prisma系统。所有符合7-T口径的大脑都被扫描,而较大的大脑则被3-T扫描仪扫描。本研究未对动物实施安乐死。脑的收集是基于以色列动物园的偶发死亡动物和国外收集的自然死亡动物。所有的动物都得到了国家公园管理局的许可(批准号:2012/38645)或在相关国家具有同等的许可。动物的大脑在死亡24小时内被提取出来,并置于甲醛(10%)中固定几天到几周(取决于大脑的大小)。在磁共振成像前24小时,大脑被放置在磷酸盐缓冲盐水中。在MRI中,大脑被放置在一个塑料盒中,浸泡在含氟油(氟化油,3 M)中,这个过程是为了尽量减少磁敏感效应造成的图像伪影。
MaMI数据库包括5名人类(3名男性和2名女性),用于所有哺乳动物的比较分析(如图2a所示)。为了进行物种内的比较(图3),作者还使用了一个包含22名人类的额外数据库(11名女性和11名男性,平均年龄为37.9岁)。没有使用统计方法来预先确定样本量,但本研究的样本量与之前的报道相似21。所有受试者(共计27人)神经健康,并签署了一份由Sheba Medical Center审查委员会和特拉维夫大学伦理委员会批准的知情同意书。分析流程与MaMI数据库中使用的流程类似。
MRI采集:
所有物种的MRI扫描方案相似,包括高分辨率解剖扫描(T2或t1加权MRI),用于解剖参考,以及扩散MRI扫描。包括高角分辨率弥散成像(HARDI)采集。HARDI数据集包括一系列覆盖整个大脑的扩散加权、自旋回波、回波平面成像图像,分别在60个(在7-T扫描仪中)或64个梯度方向(在3- t扫描仪中)进行扫描,另外还有3个非扩散加权图像(B0)。所有扫描的b值均为1000s mm2。7T的扫描机器,TR超过12000毫秒(取决于采集切片的数量),TE 20 ms和Δ/δ= 10/4.5 ms。3t的扫描,TR 3500 ms, TE 47ms士和Δ/δ= 17/23ms。保持所有物种的矩阵大小不变(128*96),对二维图像的像素分辨率(每个切片)根据大脑的大小进行线性缩放。作者进行了对照分析,以确保这个操作不会影响结果。脑切片的数量因脑形状的不同而不同,在46到68之间。不同物种的扫描重复次数和获取时间不同,取决于脑大小和信噪比。作者试图保持SNR>20,导致小的脑采集需要48h (~0.15 ml),大脑采集则约25min (~1000 ml)。信噪比被定义为大脑的平均信号强度除以噪声的sd.(图像非大脑部分的区域)。
DTI数据分析和白质追踪
作者使用ExploreDTI 22软件进行HARDI/DTI分析以及后续的全脑白质纤维重建。以下步骤用于生成纤维束:
1) 各向异性平滑(使用3像素高斯核),以降低噪声和平滑数据。
2) 运动和畸变校正:对运动、磁化率和涡流畸变在HARDI采集的个体空间进行校正。
3) 利用约束球形解卷积(CSD)方法生成了每像素的纤维定向密度函数,提供了每个体素可能的多个(n >= 1)纤维定向。使用了四阶以下的球面谐波。在使用传统的基于DTI的数据的tractography时验证了这一结果。
4) 使用对所有样本相似的CSD种子点阈值(0.2)和步长为像素大小一半的步长进行全脑的tractography。
这一步的输出是一个纤维束列表(估计的纤维束),起始和结束于任何体素(包括它们的完整轨迹)。所有能被扫描的大脑都在接下来的分析中被使用,没有被排除的数据。
白质网络的生成的分析:
由于本次研究仅对大脑内部的连接感兴趣,每个大脑的外部投射纤维(即穿过脑干的纤维)和小脑连接都被手工移除。其他的半球内投射纤维(如丘脑辐射)也包括在分析中。人工标记大脑中线,将大脑束分为左半球、右半球和半球间束三组。
为了将大脑分割成200个节点,所有的纤维端点(x y z)位置被用作k-means算法的输入。k-means算法相对于随机节点划分的优势在于,具有类似连通性配置文件的顶点将被分组在一起。k-means算法在处理未连接的网络组件时也有帮助。每个半球执行两次。将200个集群中的每个集群的中心作为网络中的一个节点。先前的研究已经表明,纤维的跟踪会导致偏误,因为纤维的绝大多数端点位于白质中。
本文的跟踪方法(包括对HARDI数据集的CSD跟踪)确保绝大多数跟踪端点(~90%)位于皮层或皮层下灰质(参见补充图12中的示例)。每个半球随机选择4000根纤维(从全部纤维束列表中)来计算网络的边缘。在所有物种的每个半球上使用固定数量的纤维,以避免由于纤维数量的不同而产生的偏差。接下来,生成一个连通性矩阵来索引任意两个节点之间的纤维连接数。
重复上述步骤100次,每次每个半球随机选择4000根纤维(作者的额外分析证实改变这个数目不会影响结果)所有的网络分析都进行了100次,然后取平均值。利用每个半球的连通性矩阵来计算半球内的MSP(MSP,mean short path,平均最短路径,分别对左右半球的网络进行估计并求平均)。使用每条纤维的端点作为节点时,网络中最大的连接组就是整个网络。此外,还计算每个节点对之间的平均距离(束长)作为连接两个节点的所有纤维的平均距离。该纤维长度还用于计算每个大脑的连接成本指数(连接矩阵和整个大脑中采样的4000个连接的长度矩阵相乘的总和)。需要注意的是,作者从所有物种中采样的纤维数量是相等的,尽管在现实中,这个数量可能不会在物种间保存。因此,本文的连接成本计量可以认为是常数数量的纤维的成本。数据的分析和收集不是分开进行的,因为没有对数据进行分组。
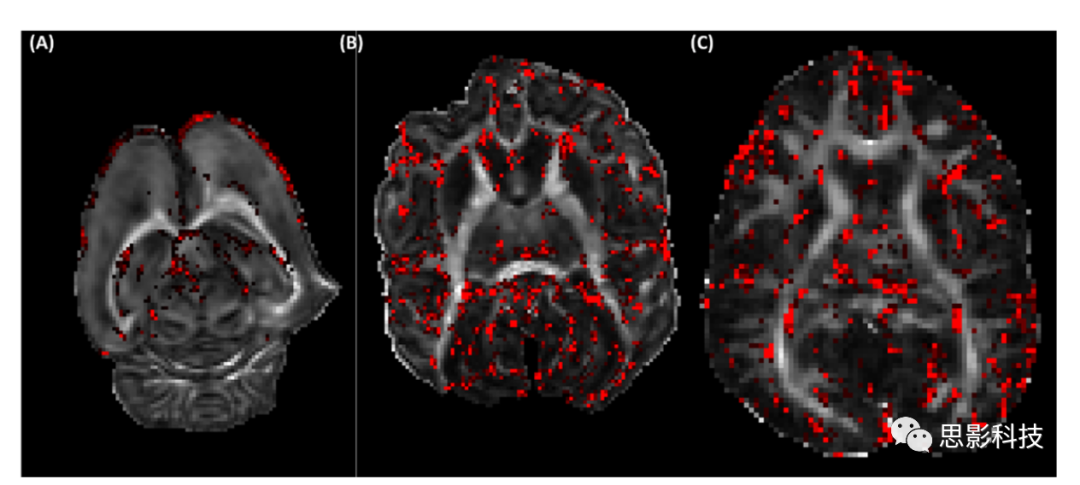
补充图12 本次研究中白质纤维追踪的端点分布示意
对扫描分辨率和采集参数的控制:
由于本次研究的扫描在所有物种中保持矩阵大小恒定,体素的维度与大脑体积成线性比例。这导致了不同样本的扫描分辨率。因此,作者进行了几项分析来验证这是一个合理的决定,包括:
(1) 比较基于dti的脑连接体和使用HARDI方法产生的家鼠的连接体的差异。两个网络之间的强相关性表明本文的方法可以重建连接体的本质(补充图13)。
(2) 以多种分辨率扫描了九个物种的大脑,可以在相对分辨率下进行分析比较 (3) 多种分辨率的分析发现,可以重建大脑中特定的纤维系统,这些纤维束的大小与大脑体积成比例。
(4) 分析了大脑中纤维交叉对结果的影响。
(5) 最后,对于4个以上标本的物种,分析发现连通性守恒原理在物种内部也存在,其绝对分辨率几乎相同(图3)。
小鼠脑白质连接体的重建:
使用艾伦鼠连接数据创建了一个追踪连接体,它可以与基于DTI数据追踪的连接体进行比较。为了在同一图谱坐标系统上对齐两个连接体,使用了一个被分割成20个皮层和皮层下区域的小鼠大脑图谱(补充图13a)。艾伦鼠连接性图谱(补充图13b)的每个投射位点都被确定并分配到这20个区域。根据Allen鼠连接数据,将每对区域之间连接的权重定义为连接强度的总和。对于基于tractography的小鼠连接体,使用了配准到同一图谱后作为数据库一部分的小鼠数据。连接体中的连通性权重被定义为每对区域之间经过的白质连接数。两个连接体如补充图13b,c所示。Mantel ’s检验各矩阵间相关性极显著(P = 2.3 *10 -4)。
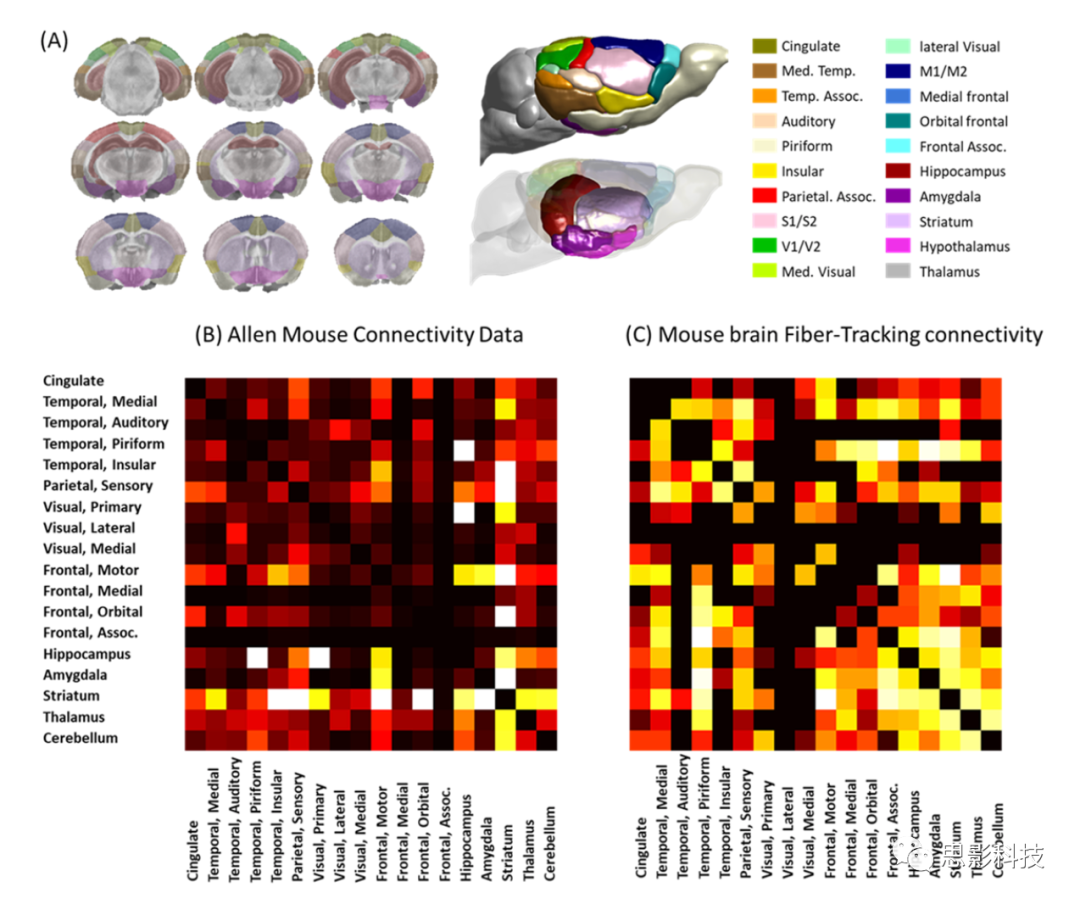
补充图13
对交叉纤维的定向分析:
为了解决多条纤维(这里指一个体素中多条纤维穿过)的定向问题(multiple fiber-orientations,MFOs),作者使用了约束球形解卷积的纤维跟踪方法(CSD方法)。利用这种分析,可以计算MFOs的体素相对于脑容量的比例。发现MFOs的比例与大脑体积呈线性关系,这表明大脑越大,交叉纤维越多。然而,本文使用的两种纤维追踪方法(CSD和传统的DTI)都揭示了相同的守恒原理(比较补充图8a和图2),尽管第一种方法可以揭示交叉光纤,而第二种则不能。这表明,纤维交叉的问题不能解释本文的主要观察结果。
估计连合纤维的比例:
对每个大脑,连合纤维被识别(仅主要的三个系统:胼胝体、前连合和海马连合,在所有哺乳动物中占绝大多数)。这是通过在正中矢状平面上放置一个感兴趣的种子区域来实现的。用这种方法得到的纤维数除以纤维总数,得到连合纤维的比例(连合比例)。由于这一比例可能会因跟踪参数而有所偏差,通过将连合系统(人工分割)的正中矢状面积(平方根)除以大脑体积(立方根)来计算连合比例的额外估计。
灰质和白质体积的计算:
当我们扫描没有头骨的大脑时,大脑的总体积是通过将噪声阈值以上的体素数量乘以图像分辨率来计算的。为了估计灰质和白质体积,将各向异性的图谱输入高斯混合模型分析,将体素分为三个组织(白质、灰质和脑脊液)。为了估计白质和灰质体积,体素(属于这两种组织类型)的概率在整个大脑中求和,并乘以图像分辨率。一个例外是人类大脑扫描(在体内进行),SPM12用于执行颅骨剥离和分割,以创建一个大脑mask来计算灰质和白质体积。
控制节点的数量:
在本研究中,作者将大脑分成每个半球100个节点。为了验证节点的数量对结果没有影响,多次运行了本文所描述的网络分析,同时将大脑分割为不同数量的节点,从50到400,每次以50递增。然后比较了不同节点下的结果。
统计分析:
所有统计分析均使用Matlab 2018 (Mathworks)进行。使用皮尔森相关系数来关联各种网络(例如MSP)和大脑参数(例如脑容量),使用P<.05为显著性水平。所有检验都是双尾的。没有对数据的正态性进行测试,因为对于像这样的大样本容量来说,这是不需要的。由于没有对样本的系统发育依赖进行校正,本文还对所有哺乳动物目进行了皮尔逊相关性分析。为了控制重复(同一物种的多个标本),使用GLM来检验半球形MSP和连合比例之间的关系。以连合比例和脑容量为固定解释因子,设定MSP为被解释变量(即因变量),进行GLM运算。使用Chow’s检验来比较人类和所有哺乳动物中MSP与连合比例回归的系数。没有使用任何随机样本检验的方法,因为除了根据它们的系统发育顺序外,数据没有进行任何分组。
研究结果:
总体来说,本次研究的结果表明了一种跨物种属目的哺乳动物大脑的连通性守恒原理,即半球间连接较少的物种,其半球内连通性更好(图1d;连合纤维的比例与脑内MSP之间有很强的相关性,与脑容量无关)。以半球内MSP为因变量,以连合比例和脑体积为固定预测因子的广义线性模型(GLM)的分析表明,半球内连接弥补了较差的半球间连接,保持了整体连接。重要的是,连合纤维的比例和半球内MSP是独立测量的,因为前者是在包括所有重建束的原始数据上测量的,而后者是在半球网络上估计的。此外,利用其横截面积估计的连合比例也得到了同样的结果,即不使用纤维跟踪算法时也得到了相通的结果(补充图 4)。除此以外,作者还通过额外的分析方法证实了这种守恒现象与纤维追踪方法以及纤维数目的约束、种子点的约束这些分析方案是无关的,这种结果在不同的扫描过程、不同的网络重构和加权参数下都获得了类似的结果(补充图5 -11,这些图大家可以在补充材料中获取和查看,不是文章的主要部分,为了不影响阅读的连续性,这里不再一一列出)。
补充图4 半球MSP与连合纤维比例的相关
注释:作者这里用连合纤维横截面的面积的平方根除以脑体积的立方根来估计连合连接的比例。与主图2不同的是,这里没有用纤维跟踪来估计连合连接的比例,而只用面积测量,所以这里的结果与跟踪算法的参数无关。R2=0.24 (Pearson相关,p<10 -13, N=232)。
总体发现,哺乳动物的大脑包括五个半球间连合纤维系统,其中主要的三个是胼胝体、前连合和海马连合。这三种纤维系统之间的半球间连接的划分具有很强的种特异性。本次发现的保护原则适用于本次研究的所有哺乳类目。由于在相关分析中没有针对系统发育进行矫正,所以作者对超过10个物种的每一目进行了单独的统计:偶蹄目:R = 0.41, P = 0.008 (n = 40);食肉目:R = 0.33, P = 0.019 (n = 51);灵长类:R = 0.39, P = 0.007 (n = 52);翼手目:R = 0.69, P = 0.00001 (n = 31);啮齿目:R = 0.64, P = 0.0001 (n = 29)。这说明,对于每个一个目种而言,这种相关都是稳定的。
为了测量连接成本,作者量化了总连接长度(即所有纤维长度的总和)。在所有哺乳动物中使用了标准化长度,每个体素相对于大脑体积都有相同的大小(具体见方法部分,作者对所有动物的大脑体素进行了针对其全脑体积的标准化,保证所有动物的体素数目是相同的)。需要注意的是,由于纤维束追踪实际上并没有测量轴突,而是测量轴突束和神经束,因此,对长度的估计反映了宏观网络的连接长度。有趣的是,所有哺乳动物的标准化连接长度并不取决于大脑的大小(图1f)。
除了上述发现,本文还发现,一个物种的大脑半球之间的连接也会有所不同,并且,连通性守恒原则也适用于物种内的差异。对来自四种不同物种(人类、猕猴、果蝠和老鼠)的多个个体的检查显示,大脑半球间连接较少的个体,其大脑半球内连接较好(图2)。这说明,本次的研究结果也适用于物种内的个体差异,由于本次研究中个体之间的扫描信噪比(SNR)和分辨率非常相似,这表明研究结果中所描述的现象不是该方法造成的伪影,该结果应该是鲁棒的。
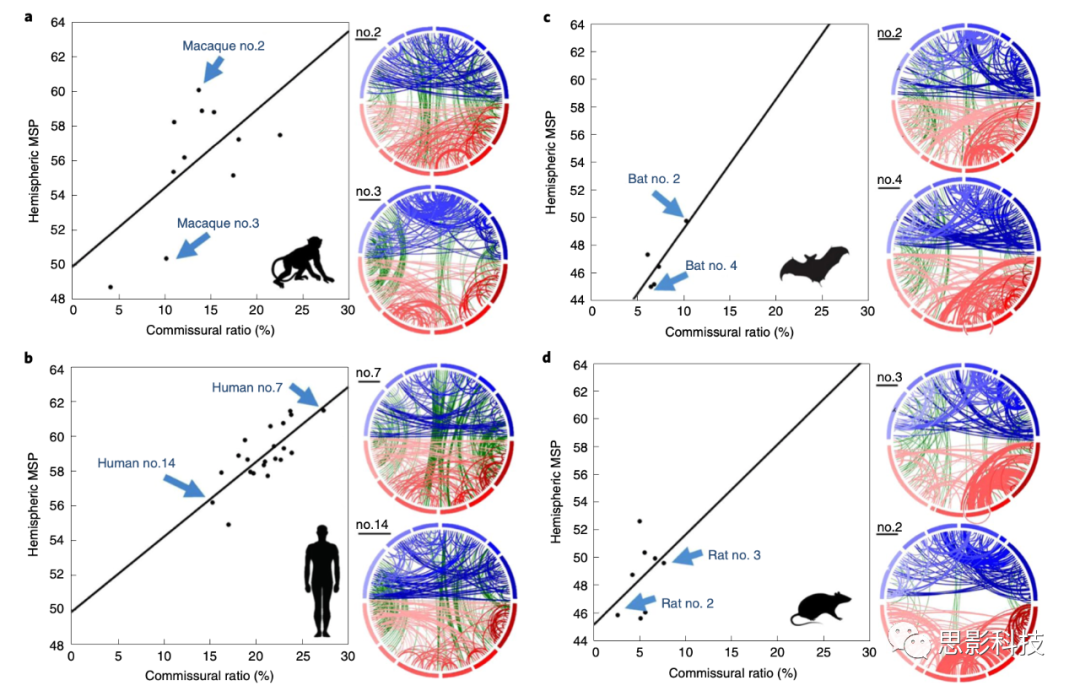
图2 物种内的个体半球内MSP与连合纤维的连合比例的相关
注释:在猕猴(a)、人类(b)、蝙蝠(c)和老鼠(d)中,半球内MSP作为连合比例的函数。两个有代表性的连接体以网络连接图的形式呈现,显示了全部200个节点的连接。两个连接体分别显示低的半球内MSP(底部)和高的半球内MSP(顶部),左半球连接为红色,右半球连接为蓝色。大脑半球之间的连接用绿色表示。节点是根据他们的大脑解剖位置(补充数据图1)。(猕猴、人类、果蝠和大鼠的皮尔逊相关效应大小;R2 = 0.31, n = 11;R2 = 0.57, n = 22;R2 = 0.22, n = 5;R2 = 0.44, n = 7)。
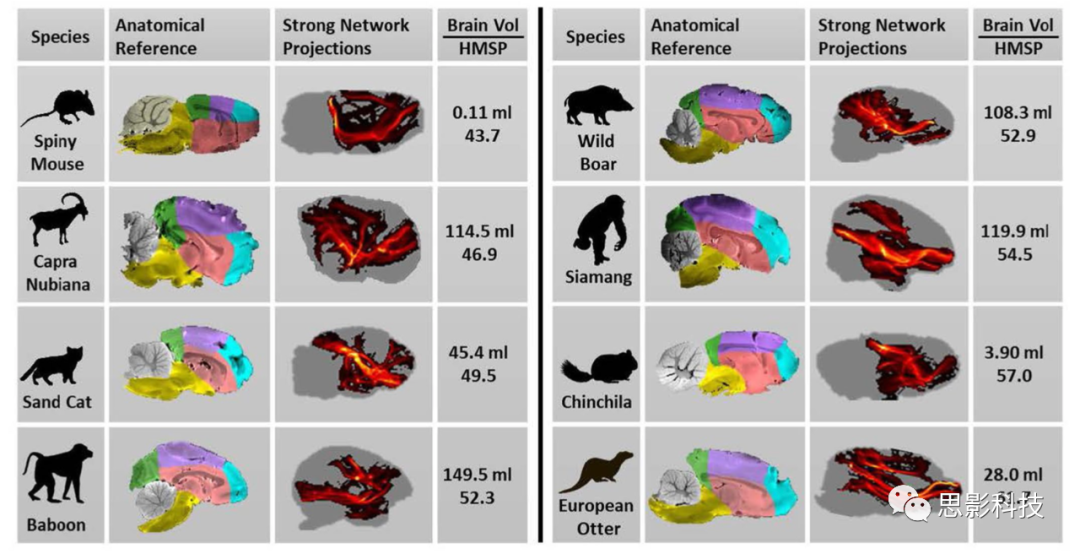
为了研究连合纤维较少的大脑如何改善半球内连接,作者还计算了每个大脑中强连接的比例,即权重超过比例中值的连接。大脑半球连接较好的大脑有更强的连接,这表明权重更强的连接是半球内连接的主要贡献者(图3a)。仔细观察强连接的网络,发现后前纵束是所有物种中最强大的连接。因此,作者在48个物种中对其进行了重构,发现其权重与MSP呈显著负相关,表明其有助于改善连通性(图3b;R2 = 0.39, P <10 -5, Pearson’ s相关检验,n = 48)。
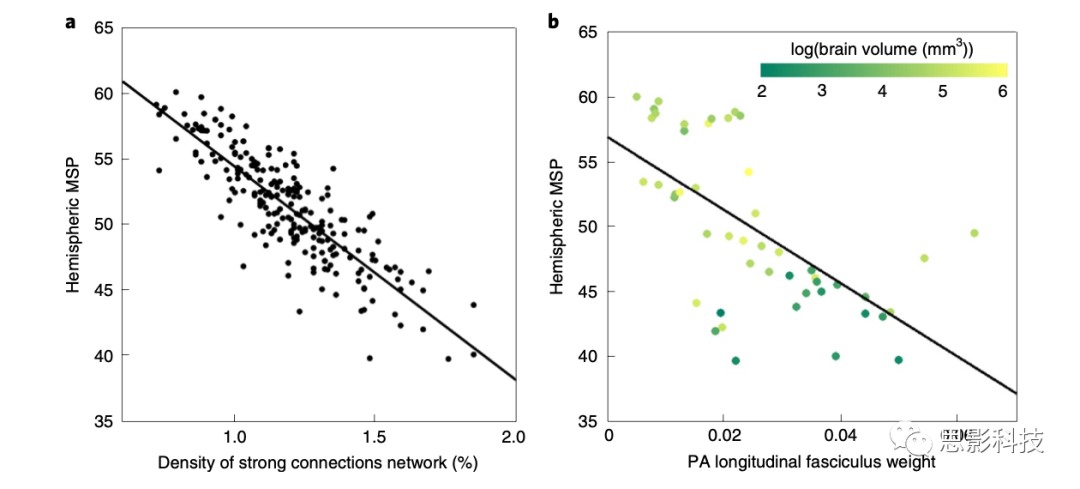
图3 强连接驱动半球内的连接
注释:a图,半球MSP与强连接网络密度呈负相关(P <10 -61 ,Pearson s相关,R2 = 0.71, n = 232)。为了揭示特定的强连接的结构特征,作者生成了一个热图,显示所有的强连接投射到一个正中矢状切片上(扩展数据图2)。四个叶的估计标志被显示出来,以供比较。这张热图表明,无论大脑体积或MSP如何,后前纵向纤维束(扩展数据图2中为浅红色)是哺乳动物中最强的连接。在48种物种中,前后纵束权重与半球MSP显著相关(其穿过的区域用彩色编码(P
<10 -5;Pearson’ s检验,R2 =
0.49, n = 48)。
拓展数据图2:强连接 在正中矢状位显示的所有的强连接的连接图
补充图14 哺乳类动物的后前纵向纤维束的图示化
研究结论:
该研究揭示了一个守恒原则,在哺乳动物中,网络连接和标准化的连接成本几乎独立于网络架构(即不同的物种存在不同连接模式,有些物种连合纤维较少)而固定。使用相对标准的(而不是绝对的)连接成本进行比较是合理的,因为大型动物可以在连接成本上会投入更多的能量。研究结果发现,这一保护原则适用于所有哺乳动物,并与大脑大小无关,表明一种选择性的进化压力有利于有效的连通性和连接成本的平衡。本观察进一步支持了这一结论,即守恒原则不仅适用于连接体的种间变异,而且也适用于连接体的种内变异。DTI有几个众所周知的局限性,但本研究的许多对照验证表明,这些局限性并不影响本文的发现和结论。
100多年前,大脑连接研究的先驱拉蒙·卡哈尔(Ramon y Cajal)提出假设,认为大脑应该节约连接成本和提升传导速度。通过大量的比较,本文能够证实这些假设。本研究收集的数据库有望揭示哺乳动物连接的更多基本原理,其中一些可能转化为认知和其他功能。偏离这些原则的物种和个体可能意味着临床问题或独特的认知功能。这方面的研究应该在未来获得更大的关注,可能会产生许多新的见解。
原文:Conservation of brain connectivity and wiring
across the mammalian class

微信扫码或者长按选择识别关注思影
如对思影课程感兴趣也可微信号siyingyxf或18983979082咨询。觉得有帮助,给个转发,或许身边的朋友正需要。请直接点击下文文字即可浏览思影科技其他课程及数据处理服务,欢迎报名与咨询,目前全部课程均开放报名,报名后我们会第一时间联系,并保留名额。
第十四届磁共振脑网络数据处理班(重庆,7.26-31)
第三十届磁共振脑影像基础班(南京,7.31-8.5)
第十届脑影像机器学习班(南京,6.30-7.5)
第十二届磁共振弥散张量成像数据处理班(南京,6.18-23)
第二十届脑电数据处理中级班(重庆,8.9-14)
小动物磁共振脑影像数据处理班(预报名,南京)
第二十一届脑电数据处理中级班(南京,9.7-12)
第七届眼动数据处理班(南京,7.26-30)
脑电信号数据处理提高班(预报名)
脑磁图(MEG)数据处理学习班(预报名)
思影科技功能磁共振(fMRI)数据处理业务
思影科技弥散加权成像(DWI/dMRI)数据处理
思影科技脑结构磁共振成像数据处理业务(T1)
思影数据处理业务三:ASL数据处理
思影科技脑电机器学习数据处理业务
思影数据处理服务五:近红外脑功能数据处理
思影数据处理服务六:脑磁图(MEG)数据处理
招聘:脑影像数据处理工程师(重庆&南京)
BIOSEMI脑电系统介绍
目镜式功能磁共振刺激系统介绍