连接组(Connectomics)用于表征脑网络中的节点以及节点之间成对的连接。节点的功能角色是通过它们与网络其余部分的直接或间接连接来定义的。但是,不能在单个节点上直接表示节点在脑网络中的语义关系(当前的处理方式是用通过计算节点中不同方面的属性来表示该节点在网络中的关系的,但不同指标都指向不同方面,不像是自然语言处理中,词汇编码可以容忍上下文的语义信息,其表征本身就已经携带语义关系信息)。
自然语言处理中的类似问题已经通过word2vec等算法得到了一定程度地有效解决,这些算法可以在有意义的低维向量空间中创建单词的嵌入及其上下文关系。在这里,作者应用这种方法来创建大脑网络中的嵌入向量表征——或者称之为连接组嵌入(connectome embeddings, CE)。CE可以表征大脑区域之间的对应关系,并且可以用于推断原始结构扩散成像所缺少的连接,例如,半球间同位连接(inter-hemispheric homotopic connections)。此外,本文建立了功能和结构连接的深度学习预测模型,并以面部处理系统为例,模拟了在整个网络上的损伤效果。CE为揭示连接组结构和功能之间的关系提供了一种新的方法。在深度学习与神经影像处理结合越来越紧密的今天,本文提出了一个更基本的对网络特征进行编码的方法,相比降维处理,这种方法可能在日后会有更大的发展空间。
除此以外,本文对word2vec的解释通俗易懂,可能对你更快地学习这种方法有很大帮助。
Introduction
生物体的神经系统由专门的大脑区域组成,每个区域都具有独特的加工能力和反应能力。 但是,这些区域并不是孤立地工作的,实际上,区域的功能作用与其在系统中其他区域的解剖连接性和生理相互作用紧密相关。通过使用网络科学的概念可以系统地分析并总结这些连接和交互作用。网络由一组元素及其二元(成对)连接组成,可以表征每个元素的连接模式。连接组提供了这样一种网络描述,将一个有机体的完整神经系统概括为一个图,它代表了神经元对或大脑区域对之间的所有连接的集合。
尽管最近在连接组映射方面取得了进步,但二元关系的结果集合本身并不能完全表示和量化网络中节点之间的高阶关系。在网络的级别中,每个节点由一个向量定义,该向量对应于其与所有其他节点的连接,并分布在高维拓扑空间中。这样的二元描述不容易进行可视化、分类、对缺失边缘和节点的预测以及了解不同网络之间的关系。尽管有许多描述性的图度量可以描述局部和全局网络特征,但其中大多数度量并非用于描述拓扑空间的特征,这个拓扑空间嵌入了这个网络的所有节点。评估网络连接模式之间的距离以及随后的特征降维可以揭示成对节点之间的相似性,但是这种方法无法捕获其他关系,例如同源性或高阶正则性。
在连接组学之外,另一个专注于元素之间映射关系的领域是自然语言处理,在自然语言处理领域中单词可以由嵌入在低维分布矢量空间中的向量表征。通过将相似的单词组合为相似的嵌入表征,此表征可以促进更高级别的自然语言处理任务。用于学习单词的向量表示的一种最新模型是word2vec,它对语言的规律性和模式进行编码。可以使用线性运算来操纵这些规则。例如,计算这样一个向量操作vec(“King”)—vec(“Man”) + vec(“Woman”)更接近vec(“Queen”),而不是其他的单词向量。重要的是,最近已经普遍使用word2vec算法来表示网络而不是文本。在网络中句子的类似物是网络中随机生成的游走序列。所得的潜在节点表征在维度相对较小的连续向量空间中可以捕获邻域相似性和社区成员信息。这些低维嵌入对于随后的旨在揭示网络节点的结构关系和相似性的机器学习应用程序很有用。
在这里,本文基于以上的优势构建了基于人脑连接组的嵌入表征(connectome embedding, CE)。其目的是在低维连续向量空间中捕捉大脑区域之间的结构网络关系,以便对它们的功能角色和关系进行推断。本文认为,CE为脑网络组数据建模提供了一种通用方法,这种方法有许多潜在的应用,包括发育、个体差异和临床/转化研究。
为了测试CE的实用性,首先,使用网络嵌入算法将弥散磁共振结构MRI连接组数据嵌入到一个连续的向量表示中,即CE(图1a-e)。接下来,本文证明CE在神经生物学上是有意义的,并且可以通过线性操作来操纵。然后,本文证明了CE(连接组嵌入)可以从结构连接预测功能连接,对于直接连接和间接连接都具有较高的准确性。最后,本文使用CEs来预测结构网络局部病变的网络级别的功能效应。
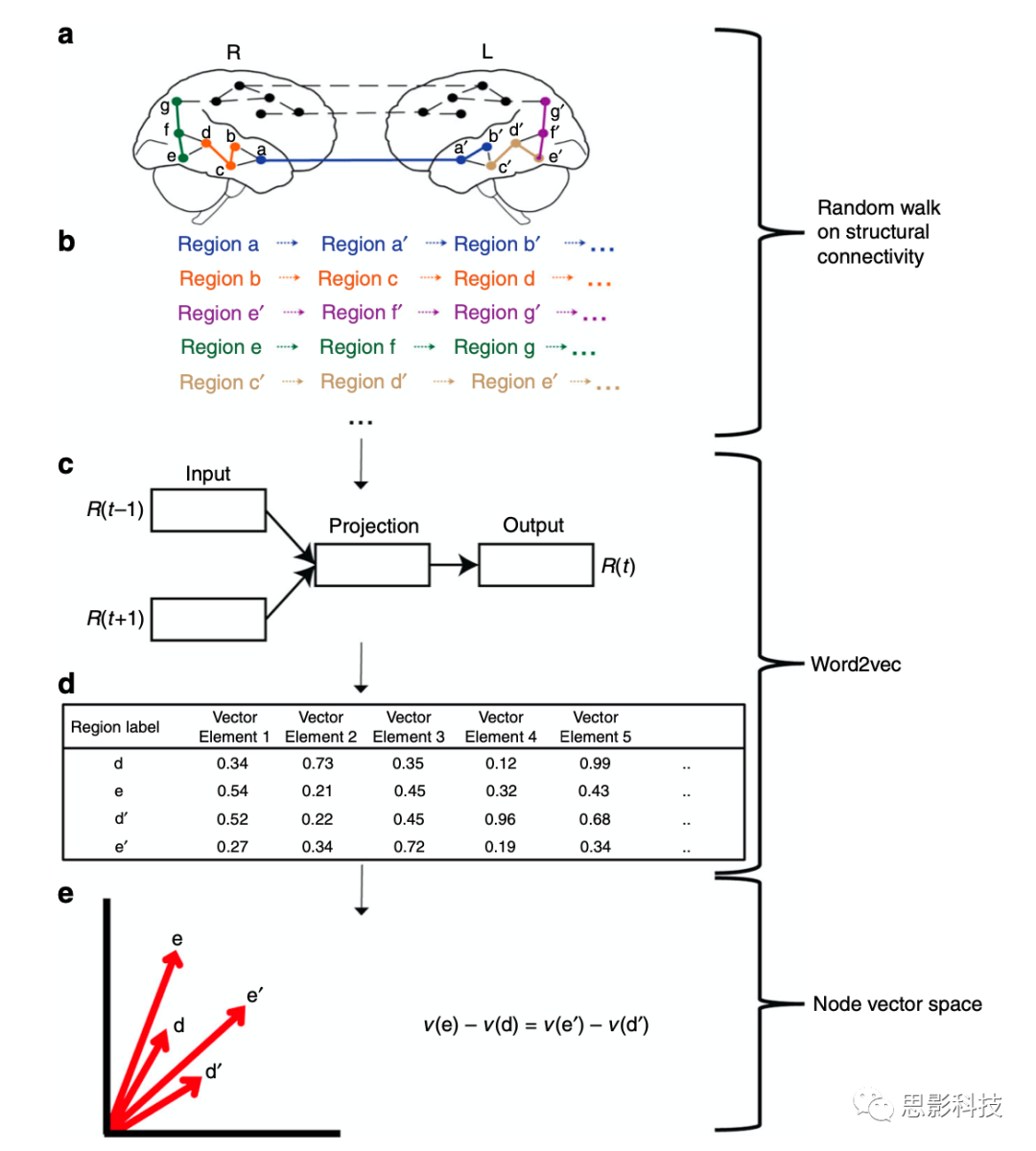
Fig. 1 构建连接组嵌入的工作流。
注释:a.连接组嵌入算法的输入是一个结构连接,用于描述大脑区域(节点)之间的成对连接。每个字母表示大脑左右半球中唯一的、对应的节点 (例如a和a '代表同伦区域)。根据结构连接矩阵,虚线表示区域之间可能的直接连边,而实线表示随机游走的路径连边。
b.使用node2vec算法在网络上执行随机游走,生成节点序列(注意,为了演示目的,这里只提供了3个步长的序列,实际序列更长)。
c.每个节点的序列被用作word2vec算法(这里使用的是Continuous Bag of Words (CBOW)算法)的输入。简单地说,对于每个序列,每个节点依次被认为是一个目标,R(t),它是由相同序列的其他节点[R(t−1),R(t + 1)..]所预测的。目标是最大化条件概率p(R(t)| R(t−1),R(t + 1)..;θ),参数theta使用2层神经网络来估计。
d.所获得的参数,即向量捕获规律,可以作为后续各种任务的基础,形成每个节点的向量分布表示。
e.这样产生的节点向量表示的方向具有拓扑意义。例如,对立半球的同源节点之间的嵌入向量之间的差异是类似的。(具体算法见Method)
Method
MRI Data.
数据集:对40个被试(数据集1)的数据集进行分析,并在100个被试(数据集2)的独立数据集上进行验证。
数据集1(Lausanne):
在收集MRI数据之前,该项目已提交洛桑大学伦理委员会[机构审查委员会(IRB)]批准。研究方案由当地IRB批准,并在纳入研究前获得每个被试的知情书面同意。40名健康被试(16名女性;25.3±4.9岁),无相关医学或精神病史,在32通道头线圈的3T西门子Trio扫描仪上进行MRI扫描。采用梯度回波(MPRAGE)序列T1加权磁化快速采集,平面分辨率为1 mm,层厚为1.2 mm。弥散谱成像(Diffusion Spectrum Imaging, DSI)包括128个扩散加权volume+ 1个参考b0 volume,最大b值8000 s/mm2, 2.2×2.2×3.0 mm体素大小,TR 6800 ms, TE 144 ms。以3.3 mm平面分辨率和3.3 mm切片厚度的梯度回波EPI序列以及TR 1920 ms和TE 30 ms记录了BOLD成像数据。
使用Connectome Mapping Toolkit处理DSI,静息态fMRI和MPRAGE数据。基于MPRAGE volume对灰白质进行分割。使用Desikan-Kiliany图谱将大脑皮层划分成83个区域。使用重建的DSI数据进行谱成像全脑结构构建。在静息态fmri采集过程中,被试躺在扫描仪内并保持睁眼9分钟。功能数据预处理包括头动矫正,白质、脑脊液和全局信号回归,线性去趋势、低通滤波等。计算每个皮层区域的平均时间信号,并使用pearson相关计算功能连接。
数据集2(Human Connectome Project;HCP);
在收集MRI数据之前,HCP扫描方案已获得圣路易斯华盛顿大学当地机构审查委员会的批准,并在纳入研究之前获得每个被试的知情书面同意。有关HCP数据集的完整详细信息之前已发布。在HCP900被试数据发布中,使用了100例无关被试进行分析。结构数据:通过使用Stejskal–Tanner(单极)扩散编码方案获得了非常高分辨率的采集(各向同性1.25 mm)。HCP DWI数据是按照MRtrix3规则处理的,并使用Desikan-Kiliany模版将全脑划分为82个区域。
功能数据:静息态fMRI(HCP文件名:rfMRI_REST1和rfMRI_REST2)是在两天不同的时间段中分别获取的,每天有两次不同的获取(左到右或LR,右到左或RL)。对于所有采集run,都使用了左右(LR)和右左(RL)相位编码中的数据来计算连接矩阵。使用HCP functional pipeline处理数据。该处理流程包括去除伪影,运动校正和配准标准空间。
MELODIC ICA用于volume数据;使用FIX识别伪影并进行去除。对volume数据和gray ordinate数据进行了伪影和与运动相关的时间过程的回归。此外,从体素时间信号中回归全局灰质信号;在正向和反向方向使用一阶Butter worth滤波器;使用workbench软件对体素时间信号进行z-score归一化,并对Desikan-Kiliany模版所划分的82个脑区中的时间信号进行平均,去除掉偏离均值3个标准差的异常时间点。计算成对节点中时间信号的pearson相关系数,为每个被试的每个fmri session计算一个对称的连接矩阵。最后将每个被试的所有的4个连接矩阵进行平均得到最终的连接矩阵。
对于这两个数据集,后续的结构连接分析和建模是基于组水平连接矩阵上的,组水平矩阵是通过对在至少25%的被试上出现的连接进行平均得到的。功能连接的组水平矩阵则是对所有被试的连接矩阵进行平均得到的。
Word and network embedding.
Word2vec算法主要包含两个模型:skip-gram和CBOW。简而言之,给定一个单词w及其上下文的语料库c,skip-gram模型的目标是通过估计参数θ来最大化条件概率p(c|w;θ);而CBOW模型的目标是通过估计参数θ来最大化条件概率p(w|c;θ)。这样产生的参数或词向量捕获了语言规律,这是后续各种任务的基础。
这里简要介绍一下word2vec算法,word2vec算法是google于2013年提出的nlp模型,其主要任务就是将单词编码为低维向量,从而可以在词向量空间中比较词与词之间的相似性。词向量具有这样的性质:1.越相似的词之间在词向量空间的夹角越小;2.词向量具有线性性质:vec(woman) - vec(man) = vec(queen) - vec(king)。如下图所示:

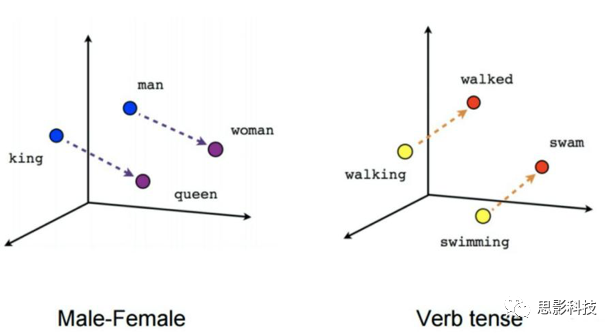
词向量具有线性操作性质
Word2vec算法本质上是一个三层神经网络,如下图所示。假设词库中单词的数量为10000,词向量的长度设定为300,下以单个训练样本为例介绍。
1. 输入词向量为长度为10000的one-hot向量,假设输入单词在词库中的顺序为i,则输入向量的第i个元素为1,其余则为0。这个单词的输入向量则为[0,...,1,...0].

Word2vec算法流程图
2. 隐藏层的神经元个数就是词向量的长度。隐藏层的参数是一个[10000,300]的矩阵。 实际上,这个参数矩阵就是词向量。这个矩阵编码了将单词从one-hot向量到词向量的映射关系。如下图所示,左边的向量为某个单词的one-hot向量,中间的矩阵则为某个word2vec算法的隐藏层参数,右边的向量则为这个单词的词向量。
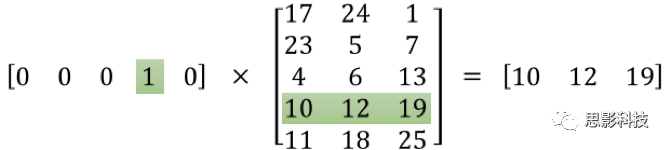
3. 输出层神经元个数为10000,即输出层的每个神经元都是对应单词的预测概率(见word2vec算法流程图)。
可以看到,word2vec其实就是利用单词预测单词来训练神经网络中间层参数以获得词向量。这里的简化模型是由一个单词预测一个单词。真实场景中,可能是由一个单词预测上下文或者由上下文预测一个单词(有点像完形填空)。这里就引出了skip-gram模型和CBOW模型。
Skip-gram模型:核心思想是根据中心词来预测周围的词。假设中心词为brown,窗口长度为2,就根据brown预测左边两个词和右边两个词。即用中心词作为神经网络的输入,周围的词作为输出。CBOW模型:与Skip-gram模型类似,只不过是由周围的词预测中心词。如下图所示

可以从图1看到,本文采用的是CBOW模型。在本文的应用中,中心词和上下文等价为连接组中的待预测节点和经过该节点的随机游走序列。
网络域中的上下文指的是网络中生成的随机游走序列。网络上序列的生成方式区分了不同的网络嵌入方法。网络节点嵌入的一种最新实现是node2vec,它使用2个参数控制随机游走的深度,允许局部或全局随机游走,从而生成节点的不同表示(图1a-e)。与利用图的谱特征的无监督特征学习方法相比,node2vec模型在一系列后续的有监督学习节点分类任务和连边预测中具有更高的预测能力。此外,已有研究表明,类似的网络嵌入算法在将所有k阶关系信息投影到公共子空间的同时,也能捕获图中每个顶点与其k阶邻居之间的k阶关系(k = 1,2,3,..)。
作者使用Node2vec和底层的Gensim python软件包在结构连接矩阵上运行CBOW node2vec算法500次,因为它可以在每次迭代中产生不同的结果。每次迭代包括800次随机游走,游走步长为20。
将嵌入向量的维数设置为30(表示节点的每个向量的长度),将确定每个节点上下文的窗口大小(来自每个节点的步长置为3。将算法参数设置为对应于局部随机游走 p = 0.1, q = 1.6)。根据连接体边缘的权重对游走概率进行加权。
利用深度学习预测功能连接
此前,Grover和Leskovec(2016)已证明Hadamard运算(向量对之间的逐元素乘法)对于学习连边特征非常有效。可以在这种情况下利用节点对表示来学习结构嵌入和功能连接之间的映射,同时采用监督学习交叉验证方案。具体而言,将平均功能连接矩阵的连边随机分为训练(75%)和测试集(25%)。利用Keras实现一个深度学习多层神经网络模型,将自变量定义为Hadamard嵌入,因变量定义为功能连接。首先通过仅使用训练集在参数空间中使用交叉验证网格搜索来优化网络架构参数。这样就产生了一个具有四层全连接的神经网络,每一层有350个神经元,dropout rate为0.1,使用ReLU函数作为激活函数,batch size为140,使用Adam优化器训练170轮。模型构建示意图如下图所示,a与a’为某两个结点的嵌入向量,进行元素间乘法后输入到神经网络中预测功能连接。
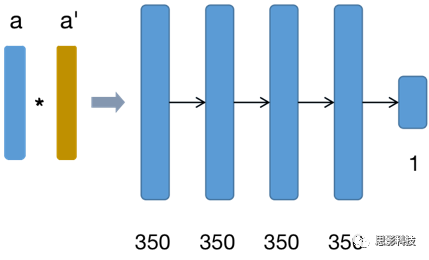
利用基于深度学习的预测模型预测因病变引起的功能表现
为了测试人工病变对功能连接的影响,首先在FFA(面孔识别区)去除后(病变后的嵌入与原始病变前的嵌入相比)构建了新的500个连接组嵌入,因为这是面部识别网络的主要枢纽。这是通过运行node2vec算法500次,并在将所有右FFA连边设置为0之后对结构连接矩阵进行随机初始化来实现的。由于嵌入向量元素可能会因权值随机初始化而发生变化(但向量之间的余弦相似度是保持稳定的),因此损伤前的网络嵌入与功能连接映射之间所学习到的映射关系不能推广为另一个连接组的嵌入。因此,本文设计了一个训练程序,其目标是学习连接组嵌入与功能连接之间的映射关系,这个映射对于权值的初始化条件是不变的。为此,这里实现了一个嵌套的交叉验证方案,在该方案中,仅使用连接和连接组嵌入的子集,在连接组嵌入的许多随机权重初始化中训练病变前结构嵌入和功能连接之间的映射,以避免数据过度拟合 。具体而言,将连接分为3部分,在每次迭代中,将其中2部分用于训练(2268条连接),将剩下一部分用于测试(1134条连接)。此外,还将500个连接组嵌入随机划分3次,连接组嵌入的90%(500个中的450个)作为训练集,10%(500个中的50个)作为测试集。仅仅对测试集中的嵌入向量和连接进行预测。此外,对病变前连接组嵌入进行训练,并对病变前连接组嵌入和病变后连接组嵌入进行预测。最后,进行了10,000次迭代的置换重采样测试,以比较病变前和病变后连接组预测之间的每条连接的差异。
Results
半球间类比测试
为了测试CE向量表征是否具有与大脑拓扑模式具有类似的特征,并且可以使用线性运算进行解释和操纵,本文设计了半球间类比测试。
人脑的基本组织特征之一是功能同伦,即在两侧同源的大脑区域之间存在对称的半球间相关性。高比例的胼胝体纤维支持功能同伦,这有助于同伦连接。此外,两个半球的结构和功能连接模式显示出高度的跨半球的相似性。因此,为了设计一个用于测试和调整连接组嵌入的基准,这里假定一个半球中每对区域之间的关系应类似于另一半球中相同的成对关系。本文在node2vec和谱嵌入这两个算法中都测试了所有节点之间所有可能的半球间类比。在每一次类比测试中,将会计算线性组合向量[vector(“Right Node A”)—vector (“Right Node B”)+vector (“Left Node B”)]与连接组中其他所有节点向量之间的余弦相似性,以捕获两个向量夹角之间的角度(注:理论上来说,如果假设严格成立,那么与线性组合向量之间夹角最小的节点向量应该是vector(“Left Node A”))。这个计算过程将生成一个余弦相似距离向量,向量中的每个元素表示线性组合向量与其他节点向量之间的余弦距离,然后按升序排列。在每一次类比测试中,期望向量(“Left Node A”)的在余弦相似距离向量中的排序(rank)会被记录下来。这里把这个计算过程称作半球间类比测试。
将根据更标准的谱嵌入算法对结果进行基准测试,该算法是一种无监督的方法,旨在通过使用图拉普拉斯算子的分解来计算数据的低维非线性嵌入。谱嵌入的基础假设之一是,互相连接的节点在向量空间中将会一起嵌入(同质性),并且这些嵌入表征可用于分类。
对于每次半球间类比测试(注:由于node2vec算法会受到参数初始化的影响,因此会计算500次减弱随机效应),计算500轮node2vec算法中期望向量的排序的中值。例如,与其他节点嵌入向量相比,vector(“Right Amygdala”) 与线性组合向量[vector(“Left Amygdala”)—vector(“Left Fusiform Gyrus”) + vector(“Right Fusiform Gyrus”)]之间的距离应当最小(如图1e所示)。如果计算出的向量确实确实最接近vec(“Right Amygdala”),则类比测试得到的排序(rank)应该为0。那么这个节点被称为期望节点(本例中为Right Amygdala)。请注意,较高的排序(rank)意味着期望的节点嵌入与所计算的线性组合向量不太相似,因此较高的排名反映了较差的性能。因此,如果在所有可能的类比测试中,较高比例的期望节点将具有较低的排序(与线性组合向量相距较小的距离),则可以推断出所获得的向量表示将包含有意义的拓扑信息。
数据集1:
在所有半球间类比测试中,有54%的预期节点,即820个(有82个同源节点的半球间类比测试的数量)中的444个,在使用连接组嵌入时被列为排名前五的节点。相比之下,使用常规谱嵌入算法,820个预期节点中只有153个节点排在前五名,占18.6%。两种嵌入方法中排名前5位的节点所占百分比差异显著,χ2(1, N = 1640) = 223, p < 2.2e-16(图2)。数据集2:与数据集1的情况一样,连接组嵌入和谱嵌入算法之间的差异是显著的。在所有半球间类比测试中,30%的预期节点,即820个中的246个(82个同源节点间可能存在的半球间类比测试对)在使用连接组嵌入时被列为排序前五名节点。相比之下,使用传统的谱嵌入算法,820个预期节点中只有108个(13%)排在前5位。两种嵌入方法中排名前5位的节点所占百分比差异显著,χ2(1, N = 1640) = 68.6, p < 2.2e-16。
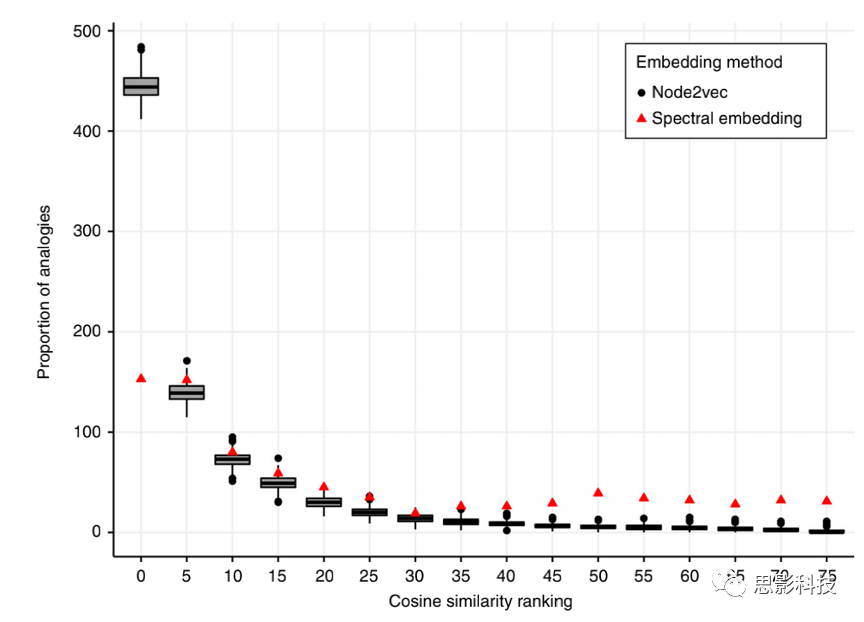
图2 两种节点嵌入算法在半球间类比测试中的性能。
备注:半球间类比测试评估了两个嵌入节点向量的表征能力,在给定一个半球中的成对关系时,以推断另一个半球中每对节点之间的关系。对所有成对节点进行类比测试,并对结果进行排序(rank),以使rank越低越好。在node2vec算法的500次迭代中,预期节点的排序以5分别进行划分。箱线图代表了500次node2vec中的期望节点的排序划分。红色三角形代表谱嵌入算法的期望节点的排序。重要的是,node2vec算法有更高比例的预期节点处于最低的排序区间中(0-5)。请注意,谱嵌入算法中有较高比例的期望节点处于较高的rank中,这表明该算法在此任务的性能较差。该结果表明,node2vec向量嵌入成功地包含了功能同伦信息。
节点表征的相似性
正如半球间类比测试所暗示的,学习到的CE载体之间的关系包含有意义的神经生物学信息。为了进一步探讨此问题并了解每对节点之间的成对关系的性质与功能同伦的关系,本文刻画了它们各自的CE向量的表征相似性。具体来说,在每对连接组嵌入向量之间计算了余弦相似度(图3)。此过程相当于对结构连接矩阵进行重建(embedding reconstruction, 嵌入重建)。这里并不期待对结构矩阵进行完美重建。相反,这里假设如果CE能够捕获高级拓扑属性,则应将其反映在CE的成对关系中。作者首先计算了每个嵌入重建(node2vec和谱嵌入算法)与使用扩散成像获得的结构连接矩阵之间的Spearman Rho(秩相关系数)。

图3 结构连接矩阵和节点嵌入的余弦相似度。
a. 具有83个预定义感兴趣区域的原始结构连接矩阵。每个格子代表一对区域之间的结构连接。
b. 原始的平均功能连接矩阵。
c. 谱嵌入重建矩阵。
d. node2vec算法重建矩阵
数据集1:
连接组结构矩阵与谱嵌入重建矩阵之间呈现弱相关,rs = 0.2,p <10-6,而与node2vec嵌入重建矩阵呈现强相关rs = 0.62,p <10-6(图3)。数据集2:类似于数据集1中测得的相关性,连接组结构矩阵与谱嵌入重建矩阵不相关rs = -0.02,p = 0.11,但与node2vec嵌入重建矩阵有很强的相关性rs = 0.63,p <10-6。
作者假设node2vec和谱嵌入重建之间的差异可能部分是由于嵌入算法倾向于根据现有的高阶关系推断丢失的连接。例如,使用扩散成像无法很好地捕获同源的半球之间的结构连接。最近,一项使用具有32,350个连接报告的分析(是根据已发表的大鼠通路追踪实验整理而来的)表明,所有皮质区域中约有三分之二发送同伦连接。因此,由于通过嵌入捕获的拓扑特征,同伦半球间连接可以在node2vec连接性重建中得到更好的恢复。
为了比较原始结构连接矩阵和重建的嵌入连接矩阵之间同位半球之间的连接数,作者对每个矩阵使用Z分数归一化,并使用阈值进行矩阵二值化。
数据集1:node2vec重建矩阵的同位半球间连接占比为73%,而在0阈值时原始结构连接矩阵中的同伦半球间连接占比为48%。 这种差异具有统计学意义(χ2(1,N = 82)= 9.76,p = 0.001)。相似的模式随着阈值提高到0.9一直存在,但是当阈值提高到1时则消失。并且node2vec重建矩阵和原始结构连接矩阵中仅分别出现44%和34%的同源半球连接。阈值为0时,谱嵌入重建矩阵(53%)和结构连通性矩阵(48%)之间同位半球间连接的差异不显著(χ2 (1, N = 82) = 0.39, p = .53)。阈值提高到0.9时也出现相似的结果。
数据集2:与数据集1具有相似的结果,node2vec重建矩阵的同位半球间连接占比为56%,而在阈值为0时原始结构连接矩阵中的同位半球连接占比为21%。这种差异具有统计学意义(χ2(1,N = 82)= 27.9,p <10-6)。 当应用各种阈值直至0.9时,出现相似的模式,但在阈值为1时这种模式消失,并且node2vec重建矩阵和原始结构连接矩阵的同源半球间连接分别为19%和12%。在较低的Z阈值(0.0–0.1)下,谱嵌入重建矩阵与结构连接矩阵之间的同位半球间连接仍然存在显著差异(χ2(1,N = 82)= 6.97和6.2,p = 0.008和 0.01)。一旦将阈值增加到0.1以上,则在任何阈值上都没有显著差异。
与静息态功能连接的关系
正如迄今为止的发现所报告的,CE可以为结构连接提供有意义的表征,因此,本文将研究其与静息态功能连接网络之间的关系。具体而言,区域时间序列之间的统计依赖性通常称为功能连通,许多先前的研究表明,长时间处于静息状态期间记录的功能连接与底层的结构连接密切相关。尽管这种静息态连接取决于底层结构,但它也表征了网络节点之间的较高级别的交互关系,而不一定由被直接的成对的结构连接捕获。例如,除了直接的解剖连接的节点之间的静息态功能连接(直接连接)之外,由于整个网络和网络之间的间接交互作用,在间接解剖连接的节点之间也存在许多功能连接(间接连接)。正如上面的分析所证实的,CE重建矩阵包含高级拓扑连接信息。这里假设,此类信息与静息态功能连接的关联性可能比原始结构连接矩阵更大,因为它可能能够捕获很大比例的间接效应。
数据集1:实际上,与功能连接和谱嵌入重建连接之间的相关性相比(rs = 0.13,p <10 -6;图4b),以及功能连接和原始结构连接之间的相关性相比(rs = 0.311,p <10-6;图4a),node2vec重建连接与功能连接之间获得了更高的相关系数(rs = 0.328,p <10-6;图4c)。重要的是,当考虑在原始结构矩阵中并未直接连接的节点对时,这里获得了node2vec重构与功能连接矩阵之间的正相关关系(rs = 0.127,p <10-6),而谱嵌入重建连接和功能连接之间没有显著的相关。 数据集2:与从数据集1获得的结果相似,node2vec重建矩阵与功能连接之间测得较高的相关系数(rs = 0.31,p <10-6;补充图3c)。功能连接与谱嵌入重建连接之间的相关性(rs = 0.15,p <10-6;补充图3b),以及功能连接与原始结构连接之间的相关性(rs = 0.21,p <10 -6;补充图3a)。在验证原始结构矩阵中的间接连接的节点时,作者测量到node2vec重建连接与功能连接矩阵之间呈正相关(rs = 0.27,p = 0.003),但谱嵌入重建连接与功能连接之间无显著相关(rs = 0.17,p = 0.069)。
这些发现表明,node2vec嵌入能够捕获与功能关系有关的重要信息,如在静息态功能连接中所测。

图4 静息态功能连接与结构连接之间的对应关系。
静息态功能连接(进行 Fisher Z变换之后)与 a)原始DSI连接矩阵之间的相关性(rs = 0.311,p <10-6)与b)谱嵌入重建矩阵之间的相关性(rs = 0.13, p <10−6) 与c) node2vec重建矩阵之间的相关性(rs = 0.328, p <10−6)
深度学习用于将结构连接映射到功能连接
为了验证重构的CE与功能连接之间的映射是否可以进一步改善,作者采用了监督式深度学习框架。利用节点对表示来学习结构嵌入和功能连接之间的映射,并采用监督学习交叉验证方案。
数据集1:当评估测试集中的预测功能连接与静息态功能连接之间的对应关系时,获得了很强的正相关性(rs = 0.6,p <10-6)(图5),并且对于直接连接(rs = 0.6,p <10-6)和间接连接(rs = 0.52,p <10-6)都存在很强的正相关。数据集2:在预测功能连接与静息态功能连接之间存在强正相关(rs = 0.52,p <10−6),并且对于直接连接(rs = 0.52,p <10−6) )和间接连接(rs = 0.6,p = 0.001)都有很强的正相关。因此,CE编码的有关间接功能连接匹配甚至超过了通过计算机模拟以及基于图分析的模型获得的先验结构-功能对应关系的大量信息。为了进一步验证,本文还进行了简单的线性回归分析。数据集1:在测试集中,预测功能连接和静息态功能连接之间呈现正相关(rs = 0.45,p <10−6),并且在直接连接(rs = 0.41,p <10- 6)和间接连接(rs = 0.32,p <10-6)的预测上都比较显著。数据集2:在测试集中,预测功能连接和静息态功能连接之间呈现正相关(rs = 0.41,p <10-6),并且对于直接连接(rs = 0.41,p <10-6) )和间接连接(rs = 0.57,p <10−6)都呈现较强的正相关。可以看到,线性相关的拟合结果弱于由深度学习拟合的结果。
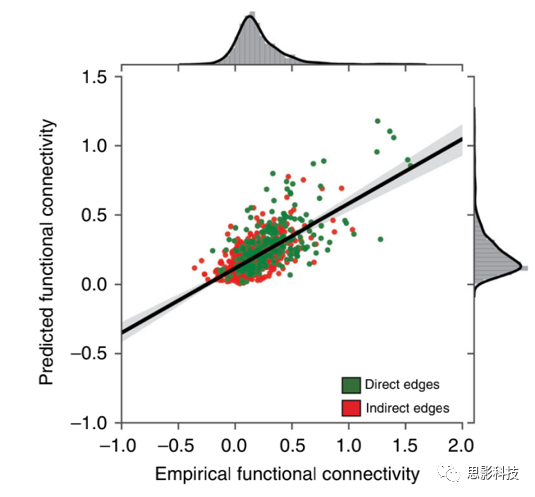
图5 使用深度学习从结构嵌入预测静息态功能连接。
绿点和红点分别标记直接连接和间接连接。当考虑所有的连接 (rs = 0.6, p < 10−6)以及直接连接 (rs = 0.6, p < 10−6)和间接连接 (rs = 0.52, p < 10−6)的时候,静息态功能连接与预测功能连接之间的相关都很显著。
FFA病变后对于功能连接的预测
连接组嵌入对于功能连接具有较高的预测性能,这种新型的预测模型可以用于理解大脑结构与功能之间的关系。一种潜在的应用是预测由于基于结构的连接组嵌入的变化而导致的功能连接的变化。具体而言,在诸如人工损伤病变或基于特定节点或连接的选择性增强等操作之后,可以创建结构连接组的嵌入表征。然后可以使用此连接组嵌入来预测经过例如人工病变等操作后的功能连接。
作者利用面部识别网络(face network)进行该应用框架的测试。面部感知是通过面部处理网络的协调活动来完成的。面部识别网络的主要枢纽之一是right fusiform face area(FFA)。该区域的病变可能导致脸盲症,一种面部识别缺陷。然而,尚未明确验证与这种病变相关的全网络效应。但是,作者的团队先前的研究表明,当被试看到完整的脸部时,诸如右FFA等关键区域将成为脸部网络的枢纽,但通过物理操作脸部(例如将人脸旋转180度),这些区域的连接性将会遭到破坏。至关重要的是,在这种中断的条件下,其他区域(right LOC,right IPS和右颞下皮质)会参与其中,并在此网络中扮演枢纽区域的角色。当先天性面部加工能力受损的人感知到完整的面部时,也会出现类似的表现。因此,作者预测,右侧FFA的损伤将模拟面部感知受损的情况,从而导致面部网络的中断,从而影响相关中枢的连通性。在这里,作者尝试模拟对面部网络进行修改,该修改可能会引发与使用人工病变的类似结果。
使用CE框架,可以估计右FFA节点(面部网络的主要枢纽)的病变如何影响整个大脑网络。通过将其所有连接都设置为零来模拟节点病变。使用10000次迭代的排列测试,作者计算了病变前和病变后所模拟的功能连接之间的差异。病变后,每条边缘的功能连接要么降低(病变前>病变后)要么增加(病变后>病变前)。
数据集1:使用节点度差异的度量来量化病变前和病变后预测的功能网络之间的差异,该差异可捕获连接到节点的重要边缘数量的差异。病变后,右侧枕叶皮质(LOC)和右侧顶下沟(IPS)增加了最多的节点度(分别增加27和9条连接)。相反,由于病变,右LOC和右颞下皮质减少了最多的节点度(分别是20和17条连接)。数据集2:病变后,右侧枕叶皮层(LOC)和右侧颞下皮层节点度增幅最大(分别增加20和14条连接)。顶下皮层的节点度排名第六。 相反,由于病变,右侧LOC和右侧海马区域表现出最大程度的节点度降低,而右侧颞下皮质仅排名第三(10条连接)。可以看到,这些模拟测试与和脸盲症相关的枢纽区域具有一致的结果(如果能做一个针对性的数据验证可能会更牛)。
请注意,这两个数据集在节点的排名上产生了一些细微的差异,这表现在在病变前后对比以及在特定的被影响的连接处的节点度提升最多。鉴于这两个数据集是完全独立的,并且具有不同的预处理流程,并且采用了不同的量度来构建结构连接(请参见方法,以了解详细信息),可以推断出这些结果之间存在这种差异。
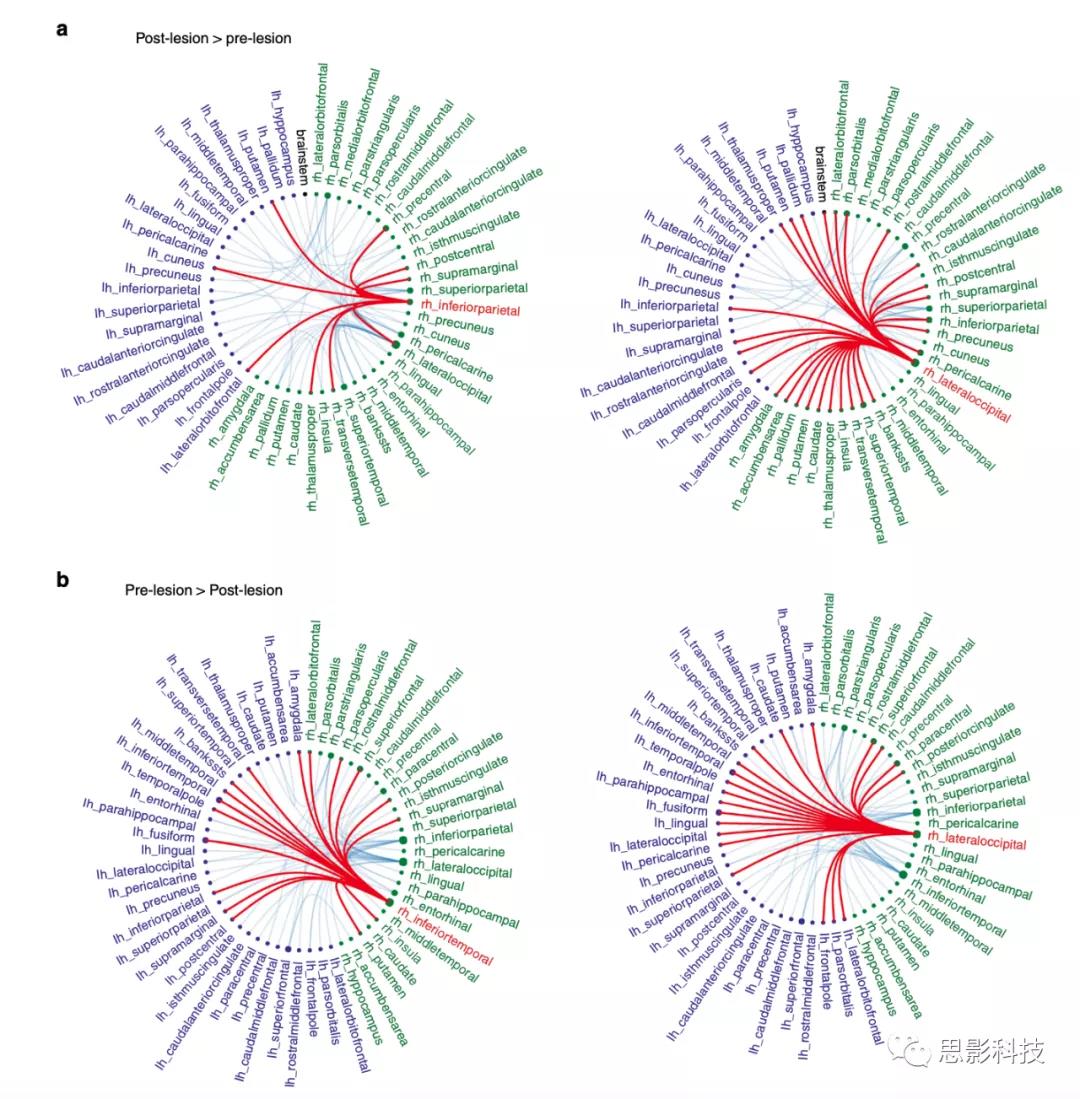
图6模拟右FFA的人工病变损伤对功能连接的影响。
绿色和紫色分别表示右半球和左半球节点,并且通过连接节点的蓝线描绘了受病变严重影响的模拟的连接差异。红色表示所选节点及其统计上的显著的连接。a. 在病变后>病变前对比中,右LOC和右IPS节点具有最高的节点度。b. 在病变前>病变对比中,右下颞皮质和右LOC节点度最高。
连接组嵌入与网络拓扑的关系
显而易见,CE捕获了重要的拓扑信息。为了研究CE与更标准的低阶拓扑度量之间是否存在潜在关系,作者计算了每个结点的CE的每个维度与若干拓扑度量之间的相关性。具体来说,作者验证了CE与节点中心度(节点度、特征向量中心度),节点的整合程度(介数)和节点的分离程度(聚类系数)之间的Spearman相关系数。结果显示,特征向量中心度仅仅与CE的两个维度具有最高的相关量级(最大Spearman相关系数ρ= 0.51,p <10-6,最小相关系数ρ= -0.57,p <10-6)。然而,CE中的数据成分与常规的图论指标(低阶拓扑度量)之间的相关值较低,并且没有明显的规律(图7)。结果中,显著的相关性似乎是零星散布的,并且它们不能解释与CE相关的大多数变异。这表明,CE捕获的网络属性超出了通过标准拓扑度量所能衡量的网络属性。
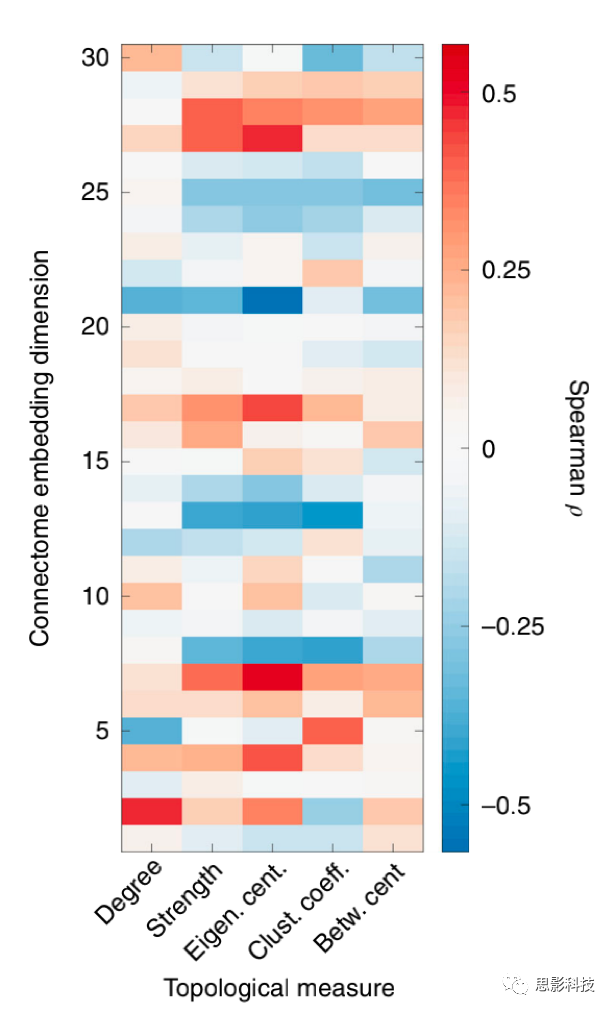
图7 不同CE维度与标准拓扑度量之间的关联。
特征向量中心度仅仅与CE的两个维度表现出最高的相关性(最大Spearman相关系数ρ= 0.51,p <10-10,最小相关系数ρ= -0.57,p <10-10)。然而,CE中的数据成分与图论度量之间的相关值较低,并且没有遵循明显的有意义的模式。
总结:
在连接组学的背景下,将词嵌入技术(如word2vec)应用于网络科学具有广阔的前景。在当前的研究中,本文证明了CE表征能够编码高维拓扑信息,例如半球间相似性。而且,CE能够以优于先前方法的水平揭示功能和结构的关系以及并实现相互预测,并且能够模拟局部网络病变对功能连接整体模式的影响。
机器学习技术与脑网络建模进行结合是一个相对较新的领域,成功应用的例子仍然有限。先前的研究大多将特征嵌入作为fMRI数据的降维步骤,并用于后续的机器学习任务,例如对精神分裂症、抑郁症、阿尔茨海默氏病和多发性硬化症患者进行分类。先前已经使用heat diffusion的平均相似性研究了结构连接之间的差异以及由于连接缺失而导致的网络退化。但是,word2vec系列模型与深度学习算法尚未在脑网络中应用。此外,这项研究第一个创建全面的机器学习框架的框架,该框架将有意义的结构嵌入转换为功能连接,从而产生了一种新颖的预测模型,该模型预测了功能连接如何受到结构连接的改变的影响,这可能对于大脑网络异常的研究非常有用。
为了测试CE向量表征是否反映了已知的大脑拓扑属性,是否能用线性操作进行解释,作者在两个独立的数据集上测试了几个基准。他们在HCP项目(100个被试)的经过严格预处理的被试子集进行了验证,并复现了主要结果。请注意,由于数据采集中的技术差异,数据集之间的预处理管道以及结构连接的构建方法均不同,这进一步增强了本文方法的通用性。最初的半球间类比测试证明,CE向量表征捕获了已知的功能同伦特征。如所预测的,一个半球中大多数区域对之间的关系类似于另一半球中相同的成对关系,其中CE方法表现出优于以前的嵌入技术的性能。
接下来,作者进一步验证了CE和结构连接矩阵之间的相关性是否反映了结构连接的高阶属性。结果证明,与原始的结构连接矩阵相比,CE重建矩阵中的同伦半球间连接更加显著,这是由于CE捕获了高阶拓扑特征,例如同伦半球间连接。此外,与原始连接矩阵相比,CE矩阵与静息态功能连接之间的相关性更高。 此外,利用深度学习算法来改善了结构到功能的映射性能。这种映射算法使得预测的功能连接与静息态功能连接之间产生了较高的相关性,不管是对于直接连接还是对于间接连接来说都有较高的相关。CE方法优于以前的结构-功能映射模型。未来的研究可能会利用相同的预测算法来预测缺失的结构连接,在这种情况下可能只有部分结构连接数据可用。
为了利用CE功能映射的高预测能力,作者进一步测试了是否有可能预测由基于结构的连接组嵌入的变化而导致的功能连接的变化。具体来说,他们将面部识别网络用作测试平台,并模拟了右FFA的结构病变。模拟结果与先前的研究发现非常吻合。基于CE的模型还预测了先前的研究中所报告的右LOC、颞下皮质和IPS之间的超连接性。与以前的工作一致,本文的发现表明,网络尺度上的功能变化可能是由局部操作(例如抑制单个节点)引起的。
本文的结果与建模框架一起,进一步迈向了在结构和功能网络变化的背景下检验因果关系的可能性。可以使用相同的框架来模拟病灶、节点、连接以及整个子网的过度表达。这样的模拟可能有助于阐明在神经发育障碍(例如自闭症谱系障碍(ASD))中发生的网络连接变化的结构基础,其中自闭症谱系障碍表现为超连通性,以及发育障碍和阅读障碍。而且,可以模拟正常的被试在不同的认知和感知需求下所观察到的网络拓扑的变化。
嵌入算法(node2vec)和当前研究中使用的参数不一定是最佳的,并且在此工作的将来扩展中有待进一步改进。本文的工作表明,CE为探索连接组数据集的高阶网络结构提供了一种有效的方法,在建模和比较人类个体差异方面具有潜在的应用价值。另一个未来的应用是使用CE来发现跨物种的大脑架构之间的关系和同源性。

微信扫码或者长按选择识别关注思影
如对思影课程感兴趣也可微信号siyingyxf或18983979082咨询。觉得有帮助,给个转发,或许身边的朋友正需要。请直接点击下文文字即可浏览思影科技其他课程及数据处理服务,欢迎报名与咨询,目前全部课程均开放报名,报名后我们会第一时间联系,并保留名额。
第十四届磁共振脑网络数据处理班(重庆,7.26-31)
第三十届磁共振脑影像基础班(南京,7.31-8.5)
第十届脑影像机器学习班(南京,6.30-7.5)
第十二届磁共振弥散张量成像数据处理班(南京,6.18-23)
第二十届脑电数据处理中级班(重庆,8.9-14)
小动物磁共振脑影像数据处理班(预报名,南京)
第二十一届脑电数据处理中级班(南京,9.7-12)
第七届眼动数据处理班(南京,7.26-30)
脑电信号数据处理提高班(预报名)
脑磁图(MEG)数据处理学习班(预报名)
思影科技功能磁共振(fMRI)数据处理业务
思影科技弥散加权成像(DWI/dMRI)数据处理
思影科技脑结构磁共振成像数据处理业务(T1)
思影数据处理业务三:ASL数据处理
思影科技脑电机器学习数据处理业务
思影数据处理服务五:近红外脑功能数据处理
思影数据处理服务六:脑磁图(MEG)数据处理
招聘:脑影像数据处理工程师(重庆&南京)
BIOSEMI脑电系统介绍
目镜式功能磁共振刺激系统介绍