系统神经科学的一个基本问题是:如何通过外部刺激,例如唤醒、睡眠、昏迷或神经精神疾病等因素,促使大脑从一种状态转换到另一种状态。这就需要对大脑状态进行准确的定义,而迄今为止对大脑状态的定义依然是难以确定的。本文中作者对功能状态进行全新的定义,在这个定义中作者针对模拟的大脑刺激如何促使不同大脑状态之间进行转换进行系统的研究。具体来说,作者使用特别的人类睡眠神经成像数据集,系统地研究在何处刺激大脑可以强制地唤醒大脑,反之亦然。作者将大脑状态定义为若干个“子亚稳态”的集合,每个子亚稳态都有一个概率稳定性和发生频率,由生成的全脑模型拟合,并在有效连接的基础上进行微调。考虑到微电路直接电刺激(DES)的生物局限性和物理局限性,本文工作选择能够确保DES诱导神经兴奋传播的连接模式,使得从复杂的脑损伤状态中唤醒成为可能。本文发表于PNAS期刊。
引言
大约13年前,认知心理学之父威廉.詹姆斯写道:“每个人都知道什么是注意力”。事实上,人类长期以来一直在识别各种“大脑状态”,包括睡眠、清醒、失语和注意力,但可以说在这些状态背后人类对“大脑状态”的认识仍然很模糊。大脑中有数十亿个神经元和数万亿个突触,在所有可能的时空水平上嵌套的递归回路中,存在大量连接和初始条件所依赖的活动进化过程。在物理学、基因组学或经济学等学科中,这些系统是复杂的动态系统,因此,复杂意味着最终的全脑行为不能仅通过研究网络的基本节点来理解。这种网络中广泛分布不断演化的动态特征是一种依赖于某些条件的自身组织,经历稳定的、“准稳定”的、高或低的活动和短暂的安排,这些动态特征被称为大脑状态。考虑到大脑状态的复杂性和它们出现的概率性,大脑状态通常是混沌的状态转换,到目前为止很少对大脑状态取得进展性的研究。
尽管如此,已经有研究者尝试对复杂的大脑状态进行解释,相关研究通过定义人类神经影像数据中的状态空间,例如对随时间移动的窗口内活动的选定时空和光谱特征的关系的估计。在这种情况下,高维信号可以减少到低维状态空间中的2或3个值,从而实现数据的可视化以及更容易的解释性。然而,尽管这些方法在理解复杂数据方面非常成功,但这种方法无法捕获状态的动态特性及其转换的过程。
根据复杂系统中的知识,大脑状态也可以被描述为网络吸引子,即相互作用的脑区之间的稳定状态,大脑状态提供对可重复和稳健的系统配置的见解,或者使用额外的生成模型来考虑不同层级的上下关系和等级相关约束。脑区间的相互作用通常反映在局部(微电路)或远端神经调节源的神经活动振荡耦合程度上。
然而,这些方法都未能给到亚稳态的概念。尽管大脑有轻微扰动的情况,但仍能暂时保持现有的平衡。显然具有高度功能分化的脑区之间的协调动态能力不太可能像观察到的单个感觉或运动系统的区域之间耦合的那么稳定和持久。稳定状态的协调模式可能经常反映动态重复出现的短期模式,这些短期模式可以存在于任何给定的亚稳态中。
在本文研究中作者提出了一种大脑状态的定义方法,称为“概率亚稳态(PMS)空间表征”,这种方法完全将子亚稳态作为常规和持续大脑状态的随机细分。这种方法可以根据发生概率和交替分布来检测和表征反复出现的子亚稳态。
这种方法可以帮助解决神经科学中的基本问题,即大脑如何在不同状态之间转换,例如从清醒到深度睡眠和麻醉,或到昏迷和神经精神障碍等疾病。解决这个问题需要考虑两方面:(1)对大脑状态的构成有更深入的理解以及对定量有正确的定义,例如对PMS空间的描述;(2)是什么因素促使大脑状态之间进行转换。这将允许使用诸如深部脑刺激(DBS)、多焦点经颅直流电刺激(tCDS)或经颅磁刺激(TMS)等外部刺激进行强制转换。
为了做到这一点,全脑模型是必不可少的,它可以将潜在的解剖学连接与从神经影像获得的动力学联系起来。作者表明,生成的全脑模型实际上可以准确地拟合对应于不同大脑状态的经验数据的PMS空间。具体来说,作者使用了一个独特的神经影像数据集,该数据集来源于健康被试入睡时同时采集的功能磁共振成像(fMRI)和脑电图(EEG)的神经影像数据。作者使用此数据集并使用马尔科夫链数据驱动分析方法发现了清醒-非快速眼动睡眠周期中不同脑网络之间的动态编码。然而,作者提供的证据表明,作者可以通过对全脑模型的模拟刺激在不同的大脑状态之间进行外部强制转换。最后,作者证明此方法可以作为一种准确的方法来促进大脑从一种状态过渡到另一种状态,特别是以此来“唤醒”大脑从深度睡眠状态到清醒状态,反之亦然。
材料与方法
实验数据:本文研究是基于在法兰克福(德国)记录的BOLD fMRI数据,在同步 EEG-fMRI扫描过程中被试保持睡眠状态。实验结果在之前的研究中已有详细描述。经当地伦理委员会批准,所有被试均给予知情同意书。在本研究中,作者只考虑了深度睡眠状态(N3阶段)的被试子集。
LEIDA:首先,作者计算了每个时间点的相位相干矩阵,以获得所有被试和条件(清醒和N3深度睡眠)在任何给定时间点的区域间BOLD同步信号量。具体来说,每个ROI的BOLD时间序列对应于明确划分的脑区和结构,经过高通滤波,随后进行希尔伯特变换,以产生每个节点(即ROI)的BOLD时间过程的阶段演变。然后通过计算相位差的余弦来估计时间t处每对n和p节点之间的相位相干性 dFC(n,p,t),如式1所示:
![]()
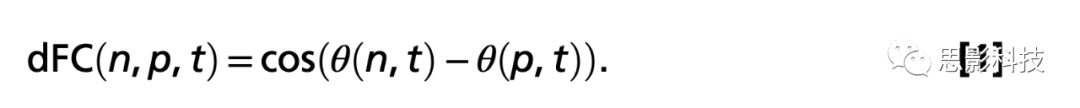
因为希尔伯特变换在极坐标中表示任何给定的信号X,![]() ,使用余弦函数,在给定的重复时间(TR)下具有临时对齐的BOLD信号(即具有相似角度)的2个节点n和p将具有接近1[cos(0°)=1]的相位相干值,而具有正交方向的BOLD信号的节点(例如一个在45°处增加,另一个在45°处减少)将具有零相位相干性[即cos(90°)=0]。每种情况下每个被试的结果dFC(t)是一个大小为N×N×T的3D矩阵,其中N=90是划定的脑区的数量,T是时间点的总数。值得注意的是,每个时间点的相位相干矩阵dFC(t)是无向的,因此是对称矩阵。后一个属性允许通过在每个时间点计算其主要特征向量V1(t)来显著降低相干矩阵的维数。大小为N×1的前导特征向量捕获dFC(t)的瞬时主导连接模式,这可以通过计算其外积V1.V1T轻松观察到。与传统方法相比,该策略显著降低了数据的维度,即将维度从N×N到N×1。
,使用余弦函数,在给定的重复时间(TR)下具有临时对齐的BOLD信号(即具有相似角度)的2个节点n和p将具有接近1[cos(0°)=1]的相位相干值,而具有正交方向的BOLD信号的节点(例如一个在45°处增加,另一个在45°处减少)将具有零相位相干性[即cos(90°)=0]。每种情况下每个被试的结果dFC(t)是一个大小为N×N×T的3D矩阵,其中N=90是划定的脑区的数量,T是时间点的总数。值得注意的是,每个时间点的相位相干矩阵dFC(t)是无向的,因此是对称矩阵。后一个属性允许通过在每个时间点计算其主要特征向量V1(t)来显著降低相干矩阵的维数。大小为N×1的前导特征向量捕获dFC(t)的瞬时主导连接模式,这可以通过计算其外积V1.V1T轻松观察到。与传统方法相比,该策略显著降低了数据的维度,即将维度从N×N到N×1。
在计算每个TR的相位相干矩阵dFC(t)的主要特征向量后,作者分析的下一步是确定可能反映亚稳态的循环FC模式。通过对包括所有被试在内的清醒和深度睡眠fMRI数据中的主要特征向量V1(t)进行聚类,以检测到离散数量的FC模式。k-means聚类算法运行时聚类个数k从2到8不等。对主要的特征向量进行聚类会产生k个N×1维的簇质心向量Vc和外积VcVcT,其代表每个集群中的主要连接模式,Vc中的元素描述了每个节点(ROI)对社团结构的贡献。为了便于子亚稳态的可视化和可解释性,使用人类连接组项目HCP的处理pipeline将簇质心向量 Vc渲染到皮层表面,根据确定最优聚类个数的标准(例如轮廓系数)发现,条件概率之间显著差异的最小P值的最佳聚类数为k=3。
在识别子亚稳态之后,作者计算了每个条件下每个FC状态的发生概率。发生概率是分配到给定簇质心Vc的迭代数除以每个实验条件下的迭代总数(TR)的比率(在所有实验条件下都相同)。
此外作者计算了TPM(状态转移概率矩阵),它以定向方式捕捉PMS(亚稳态发生概率)动力学的轨迹。更详细地,它表示给定子状态(行)转为其他子状态(列)的概率。使用基于排列的配对t检验对条件之间的发生概率和转变概率的差异进行统计评估。对于1000个排列中的每一个应用t检验来比较总体,并使用显著性阈值α= 0.05。
全脑计算模型。作者通过使用Hopf计算模型模拟了全脑水平的BOLD活动,该模型模拟了脑区之间的相互作用所产生的动力学,这些区域被认为是在已建立的解剖SC图表的基础上相互关联的。该模型由90个耦合动态单元组成,代表来自上述AAL分区的90个皮质和皮质下大脑区域。每个大脑区域的局部动力学由超临界Hopf分岔的正常形式描述,也称为Landau-Stuart振荡器,它是研究从嘈杂到振荡动力学转变的典型模型。当使用大脑网络架构耦合在一起时Hopf振荡器之间的复杂相互作用已被证明可以成功复制在电生理学、脑磁图和 fMRI中观察到的大脑动力学特征。
非耦合节点n的动力学由以下一组耦合动力学方程给出,它描述了笛卡尔坐标系中超临界Hopf分岔的标准形式:
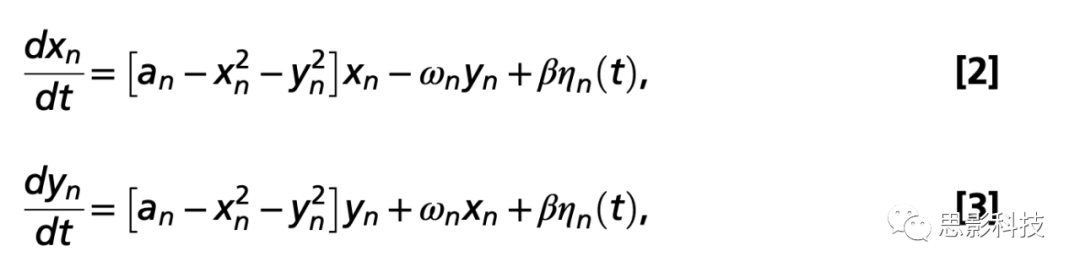
![]()
其中ηn(t)是具有SDβ的加性高斯噪声,这种正规形式有一个超临界分岔an=0,所以如果an>0,系统进入一个稳定的极限循环,频率fn=ωn/2Π。当an<0时,局部动力学处于一个稳定的固定点,代表一个较弱活动时的嘈杂状态。在这个模型中,每个节点的固有频率ωn在0.04到0.07Hz频带内(n=1, . . ., 90)。固有频率是从数据中估计出来的,由每个大脑区域的窄带BOLD信号的平均峰值频率给出。为了模拟全脑动力学,作者添加了一个附加耦合项,表示在节点n中从每个其他节点p接收到的输入,由相应的SCCnp加权。这个输入是使用公共差分耦合建模的,它近似于一般耦合函数的最简单(线性)部分。因此,全脑动力学由以下一组耦合方程定义:
![]()
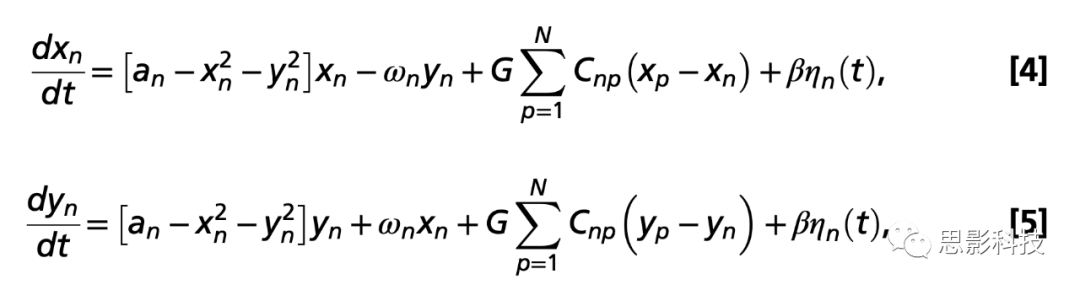
其中G表示全局耦合权值,平均缩放每个脑区接收到的总输入。作者将噪声SD固定为β=0.02,将平均SC固定为<C>=0.2。当振荡器弱耦合时,未耦合振荡器的周期轨道被保留。值得注意的是,作者在此不讨论非线性耦合的情况,在这种情况下,应考虑全耦合泰勒展开之后的下一个非零高阶项(泰勒展开是个数学计算方法,用来将一个函数表示为泰勒级数)。变量xn模拟每个节点n的BOLD信号。全局耦合参数G是作者将模型调整到动态工作区域的控制参数,在该区域模拟最佳地拟合经验数据。
经验拟合
比较经验和模拟的平均静态功能连接。通过计算经验和模拟的总平均功能连通性(FC)的上三角部分的相应元素之间的Pearson相关系数来衡量比较。
比较经验和模拟FCD。作者测量经验矩阵和模拟FCD矩阵的上三角元素之间的KS距离。对于收集M个时间点的单个被试的扫描过程,相应的基于相位相干的FCD矩阵定义为M×M对称矩阵,其(t1,t2)由2个矩阵dFC的上三角部分之间的余弦相似度定义为dFC(t1)和dFC(t2)。对于2个向量p1和p2,余弦相似度由(p1.p2)/(||p1||||p2||)给出。稳定的FC(t)配置迭代次数在FCD对角线周围反映在相关性升高的FC(t)块中。KS距离量化了2个样本的累积分布函数之间的最大差异。比较经验和模拟概率亚稳态空间状态测量。为了比较子亚稳态的概率,即聚类后提取的经验中心的概率,作者使用了模拟和经验对应概率之间的对称KL距离,即:
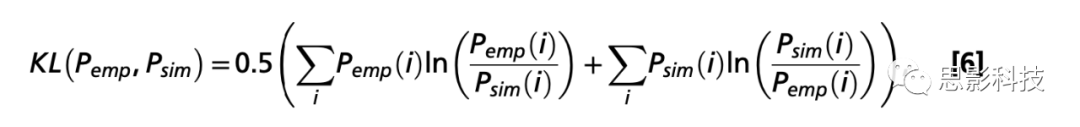
![]()
其中Pemp(i)和Psim(i)是相同经验提取的子亚稳态i上的经验和模拟概率。
比较子亚稳态之间的经验和模拟转移概率。作者计算了具有N个状态和转移矩阵P的马尔可夫链的熵率S。熵率S和Si由下式给出:

![]()
概率P(i)表示状态i的平稳概率。对于马尔可夫链的实现,每个状态的概率收敛到平稳分布P,它是以下方程的解:

![]()
因此,平稳分布是相关特征值等于1的转移矩阵的转置的特征向量。进行大量转移的马尔可夫模型具有大的速率熵,而几乎没有转移的马尔可夫模型具有低熵。对于每个转移矩阵,作者得到平稳分布,然后计算熵率。比较两个TPM(状态转移概率矩阵)的最终度量仅由两个相应马尔可夫熵值之间差异的绝对值定义。
更新EC的方法。作者推导出2个全脑模型,即1个用于计算清醒状态,另一个用于计算N3深度睡眠状态。在这两种情况下,作者优化了大脑区域之间的EC。具体来说,作者计算模型FCphases_modij和经验FCphases_empij大平均相位相干矩阵之间的距离,并用梯度下降方法分别调整每个结构连接,从而将结构转换为有效连接。该模型使用更新后的EC(有效连接)重复运行,直到拟合收敛到一个稳定值。
作者从使用dMRI的概率纤维束成像获得的解剖连接开始,并使用以下程序进行更新:
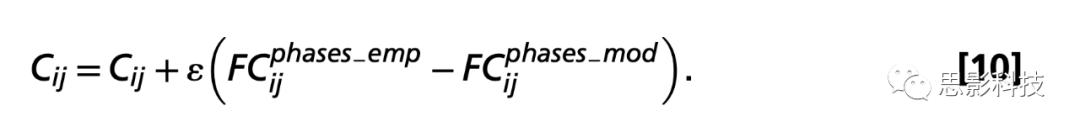
![]()
作者更新所有连接以访问使用dMRI获得的解剖连接的潜在缺失组件,已知它会错过对侧半球的连接,因为大多数已知的束是双侧的。作者使用ϵ=0.01并且总平均相位相干矩阵定义如下:
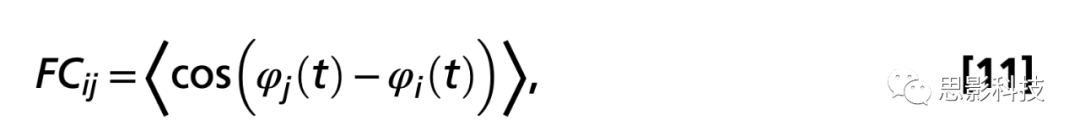
![]()
其中φj(t)是在时间t用希尔伯特变换提取的大脑区域j中BOLD信号的相位,括号表示跨时间的平均值。
结果
为了找到准确的方法来促进大脑从一种状态到另一种状态的刺激驱动转换,作者首先提供了描述大脑状态动力学的定量表征方法,称为PMS(亚稳态发生概率)空间表征方法,然后将整个大脑模型与之匹配。最后,作者进行详尽的研究旨在找到促使一种特定大脑状态转换到另一种大脑状态的最佳刺激策略。
作者第一步是使用先进的特征向量动力学分析(LEiDA)方法来识别PMS空间。使用FSL工具用于提取、预处理和求自动解剖标记(AAL)模板中定义的90个感兴趣区域(ROI)的血氧水平依赖(BOLD)信号的均值,它们包括被考虑用于估计动态连接的皮质和皮质下非小脑ROI。每个ROI的平均BOLD时间序列经过希尔伯特变换以产生脑区信号的相位演变,每对节点在任何给定时间的相位相干性可以定义为相位差的余弦,其值在1到-1范围内变化,信号分别以完全相同或相反的方向变化。此过程生成N×N×T大小的3D矩阵,其中N=90,T表示在所有考虑的扫描过程中得到的图像个数。对所有大小为N×N的动态功能连接(dFC)矩阵进行聚类,原则上可用于得到亚稳态。然而,对相干矩阵降维可以显着提高信噪比和任何关于大脑状态的聚类或分类的性能。因此,作者使用了上述LEiDA方法,该方法依赖于每个N×N相干矩阵的前导特征向量。
该方法依赖于提取每个dFC矩阵的第一个大小为N×1的特征向量V1,通过应用跨时间点和被试的聚类方法,从这个特征向量可以可靠地检测出dFC模式。由于dFC矩阵的对称性,每个特征向量可以依次用来估计相应的dFC矩阵。得到的每簇的质心定义了“子亚稳态”,作者计算聚类质心的概率,以及它的转换概率。
作者对两种不同的大脑状态使用这种方法:通过fMRI和EEG测量正常人的清醒和深度睡眠状态。根据轮廓准则确定的聚类结果显示,3个子亚稳态是拟合两种大脑状态的最佳状态。然而尽管计算代价非常大,但完全有可能将整个大脑模型与更多的子亚稳态相匹配,从而潜在地揭示更多与睡眠有关的已知的网络。在这里,作者使用3个子亚稳态进行证明。
图1总结了大脑状态的定义方法和诱发大脑状态转换的潜在策略,展示了给定情况下大脑状态(例如清醒、睡眠、麻醉或疾病)的概率状态空间。
为了促使大脑状态之间的转换,作者提出了一个框架,首先描述大脑状态(图1),然后使用全脑模型生成这种大脑状态(图2A),并最终试图促使它们之间进行转换(图2B)。这个框架中的每一个点都代表了整个大脑在某个时间点的瞬时变化,反之“云”描述了整个大脑的状态,比如在清醒或深度睡眠时的状态(参见讨论部分)。在图1D中,概率点被投影到二维空间进行可视化。
通过对图1D中的概率点进行聚类,可以从一组点生成子亚稳态并显示它们的概率(图1D最左边的面板)。由于这些群体仍将随着时间的推移而变化,所以称之为PMS空间。在图2A中,作者展示了如何将全脑模型拟合到PMS(亚稳态发生概率)空间,PMS空间提供了潜在fMRI时间序列的时空动态的概率描述。全脑模型通过调整自由参数(扩散磁共振成像(dMRI)解剖学纤维的有效电导率)将功能动力学(由fMRI数据导出)连接起来,以提供模拟和经验的PMS空间[使用适当的概率距离测量,即对称的Kullback-Leibler(KL)距离]之间的最佳拟合。在图2B中,作者展示了如何彻底扰乱和刺激全脑模型,以促进两种不同大脑状态之间进行特定转换。具体来说,接下来作者讨论将全脑模型拟合到PMS(亚稳态发生概率)空间的策略,并诱导从一种特定的大脑状态转换到另一种特定的大脑状态的策略。
![]()
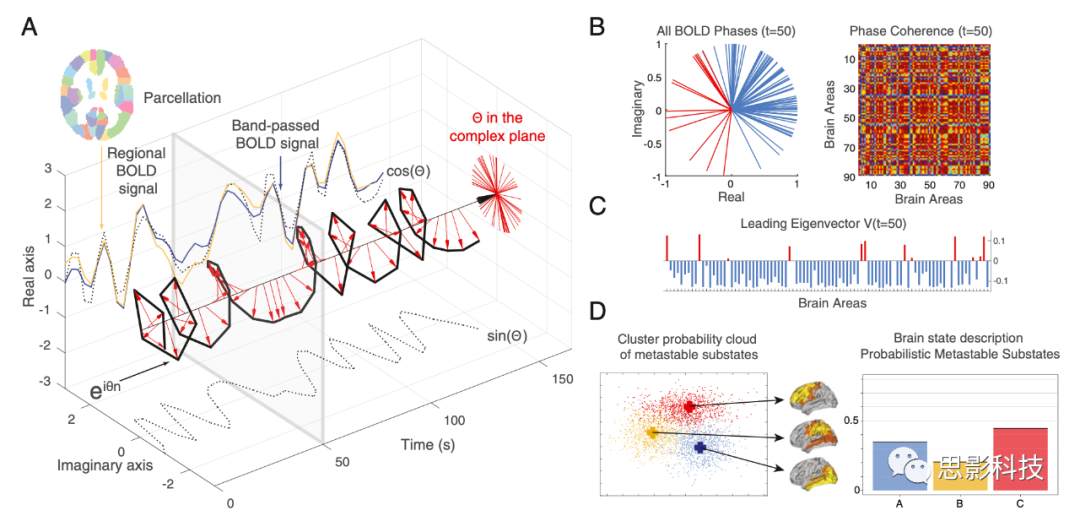
图1. 计算全脑活动的概率亚稳态(PMS)空间。
简而言之,作者使用特征向量动力学分析(LEiDA)方法,(A)其中对于每个时间点t,在每个被试的每个脑区中提取BOLD信号,计算BOLD信号的相位,以及(B)计算大脑区域之间的BOLD相位相干矩阵dFC(t),并且(C)提取该矩阵的主要特征向量V1(t)。(D)为了获得概率亚稳态(PMS)空间,作者取所有被试所有时间点的主要特征向量,并使用算法对它们进行聚类。更具体地说在A中,作者从AAL模板中显示每一个脑区(以不同颜色显示),然后提取给定区域(此处为橙色)的粗体信号。对于每个脑区,原始 BOLD信号(橙色)首先在0.02和0.1Hz(蓝色)之间进行带通滤波,然后转换为解析信号,该信号可以用其时变幅度A和相位θ表示(与实部和虚部)使用希尔伯特变换。希尔伯特相位θ可以在复平面中随时间用eiθ表示,其中实部由cos(θ)给出,而虚部由sin(θ)给出(黑色虚线)。红色箭头代表每个TR的BOLD阶段,可以看出大部分原始BOLD信号被BOLD相位cos(θ)(虚线)捕获。
(B) 对于给定的时间点(A中t=50处显示的灰色框),左图显示了复平面中表示的所有90个AAL模板中的BOLD阶段(即具有实轴和虚轴的单位圆,其中所有相位都以同一原点为中心)。右图显示给定时间t的相位相干矩阵,每对脑区之间具有BOLD相位相干 (PC)。
(C)该相位相干矩阵在时间t的领先(即最大幅度)特征向量V1(t)是最能捕捉所有BOLD相位主要方向的向量,其中V1(t)中的每个元素对应于BOLD阶段在每个区域的投影到V1(t)。V1(t)中的元素根据它们的符号进行着色(红色为正,蓝色为负,所有相位表示中的颜色方案相同)。
(D)最后为了确定PMS空间,作者收集所有被试的所有主要特征向量V1(t)作为BOLD相位相干模式的低分辨率表示,然后使用聚类算法(k-means)将样本划分为特定数量的k个簇(k=3)。每个簇都由一个中心向量(蓝色、橙色和红色)表示,作者用这些中心向量表示给定概率发生的相位相干或子亚稳态的循环模式。因此,任何大脑状态都可以由这个PMS空间表示。
全脑模型与PMS空间的最佳时空拟合
全脑大尺度模型由代表局部脑区的局部节点组成。不同脑区的连接受脑区之间的结构连接(SC)的限制。SC矩阵可以通过弥散MRI和锥体束示踪成像技术获得,而每个局部脑区组成的网络的动力学可描述为一个超临界Hopf分支的正常形式,也称为Landau-Stuart振荡器,可以对全脑模型的内部参数(如节点间的耦合强度)进行优化以拟合PMS空间。
实际上,这里的策略是使用聚类簇的经验中心来定义亚稳态,并基于这些经验中心来计算模拟的概率测量。用这种方法,作者保证了概率测量与经验亚稳态完全对应。
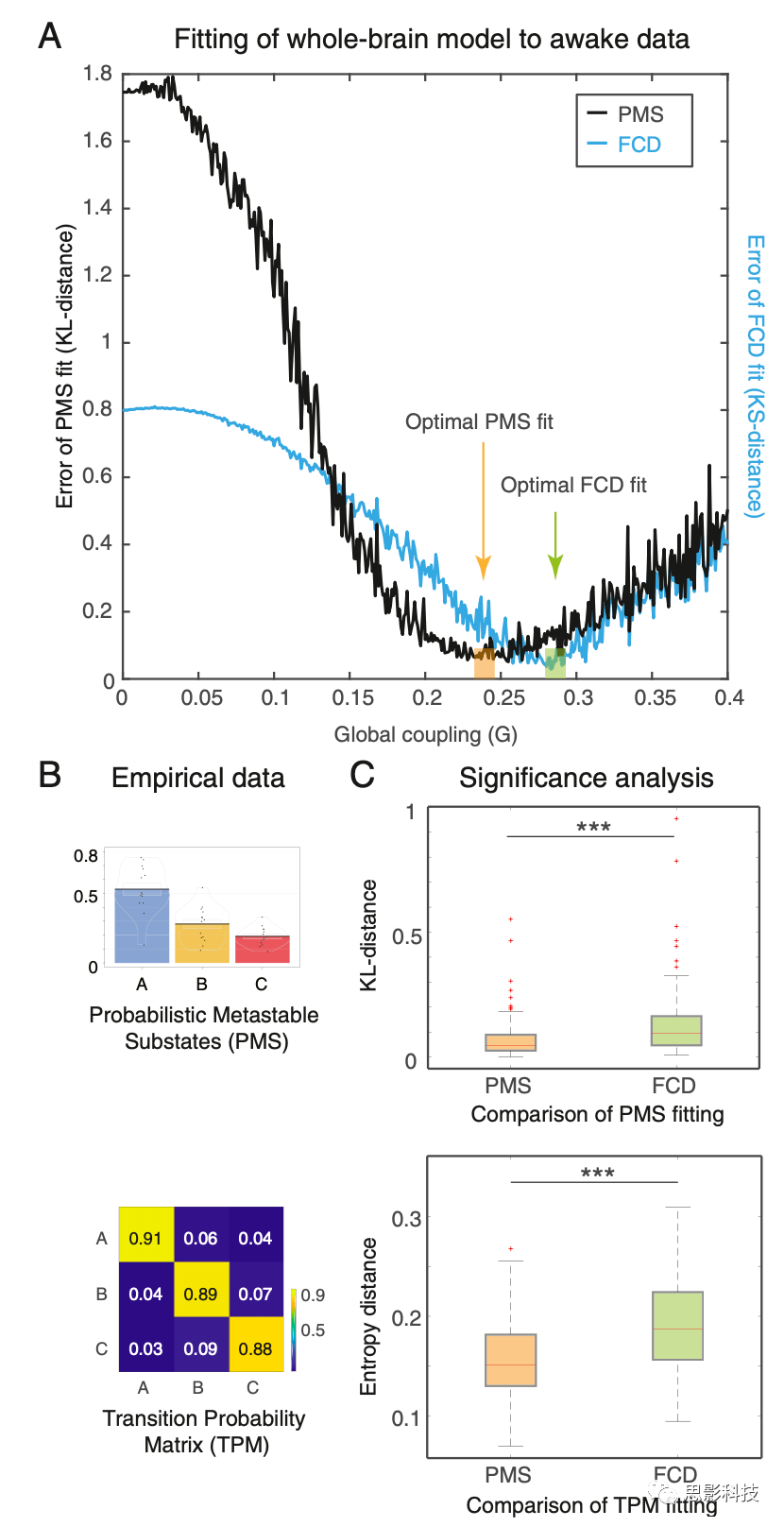
图3A为全脑模型拟合清醒状态数据的性能。在这种情况下作者详尽地研究了度量脑区间的耦合参数G,从而确定了系统的动态点。耦合参数G衡量了SC中表示的纤维密度,可以解释为轴突电导率的指标,假设轴突在大脑中与长程连接相关的电导率是相等的,髓鞘密度相似。
图3A显示了拟合G函数的2个度量值:(1)基于相位相干的功能连接动力学(FCD);(2)PMS(亚稳态发生概率)。第一种方法是收集时间分辨相位相干连通性dFC(t)矩阵的上三角元素(所有被试),然后使用Kolmogorov-Smirnov(KS)距离将这些经验分布与模型中相应的模拟分布进行比较。该KS距离的最小值对应于对时空特征的最优拟合,在G=0.283处得到。在这种情况下,当全脑模型与FCD拟合时,最优最小值并不是PMS特征的时空动态的最佳拟合。
相反在第二种情况下,作者通过提取经验性的PMS获得了更准确的结果,如图3B所示,带有PMS空间以及转移概率矩阵(TPM)。为了找到PMS(亚稳态发生概率)的最优最小值,作者计算了由来自同一经验质心的模型生成的经验概率与模拟概率之间的对称KL距离。这是一个严格的标准,以确保能够获得最佳的拟合效果。事实上,经验数据的最佳PMS拟合是在G=0.245最小值处获得的,这显然优于FCD(图3C,上)。此外,用马尔可夫熵距离测量的转移概率也明显更好地拟合(图3C,下)。请注意转移概率矩阵的对角线值(即保持相同状态的概率)远高于转换状态的概率。这很重要,因为它反映了子亚稳态的特性。
总体而言,这些结果表明,基于PMS(亚稳态发生概率)的表征大脑状态的测量方法提供了全脑模型中最准确的工作点,以解释定义大脑状态的大脑活动的最详细的时空动力学特征。
![]()
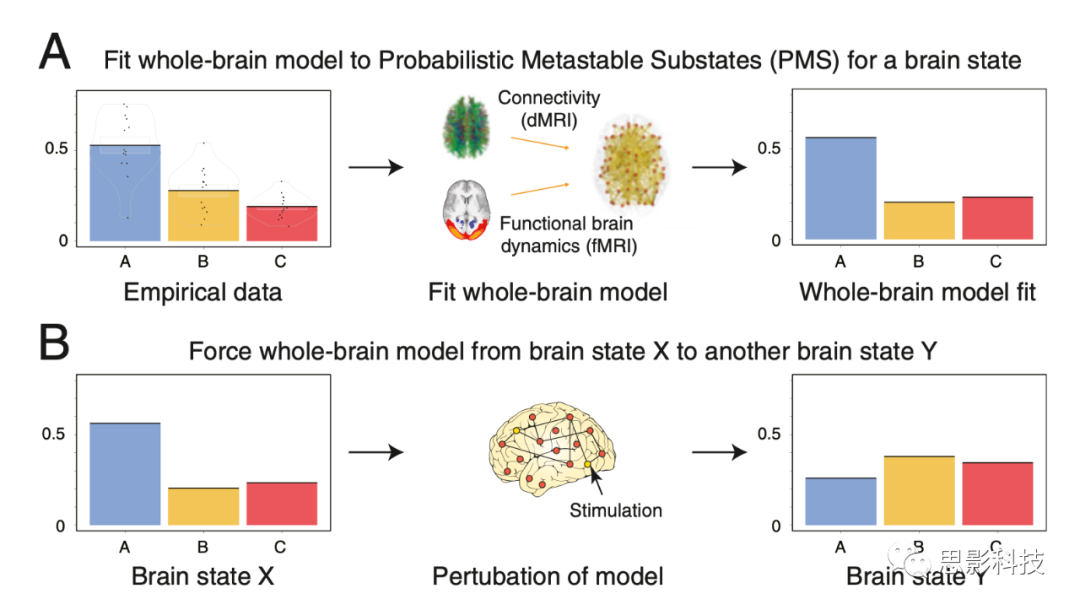
图2. 模拟大脑状态并强制在不同大脑状态之间转换的示意图。这个过程包括3个步骤。(A) 首先,根据PMS空间(使用图1所示的方法)表征给定的大脑状态,产生了3个不同的子状态(蓝色、橙色和红色),它们具有与每个子状态相关联的不同概率。其次,作者将全脑模型直接拟合到PMS空间。(B) 第三,原大脑状态X的全脑模型可以被彻底扰动和刺激,以促进和强制特定转换到目标大脑状态Y。
![]()
图3. 全脑模型与静息状态清醒功能磁共振数据概率状态空间拟合结果。 (A)当改变单个全局耦合参数G时确定拟合,该参数测量了SC中表达的纤维密度,可以解释为每个单个纤维的突触电导率。在这里,作者展示了2个拟合函数的测量方法:(1)基于相干的函数连通性动力学(FCD)和(2)概率子亚稳态(PMS)空间。通过计算科尔莫戈罗夫-斯米尔诺夫(KS)距离(黑线),可以找到FCD的最佳拟合,而使用相同的经验概率和模型使用相同的经验质心生成的模拟概率之间的对称Kullback-Leibler距离(KL)距离,可以计算对PMS空间的拟合,PMS的最佳拟合值为G=0.245。 (B)作者展示了当使用3个子亚稳态时的PMS空间和TPM(状态转移概率矩阵)。
使用有效连接优化全脑模型
时空PMS(概率子亚稳态)空间建模的第三步是针对两种完全不同的大脑状态获得两种不同的优化全脑模型。作者使用了两种自然发生的显著不同的状态,即清醒和深度睡眠。
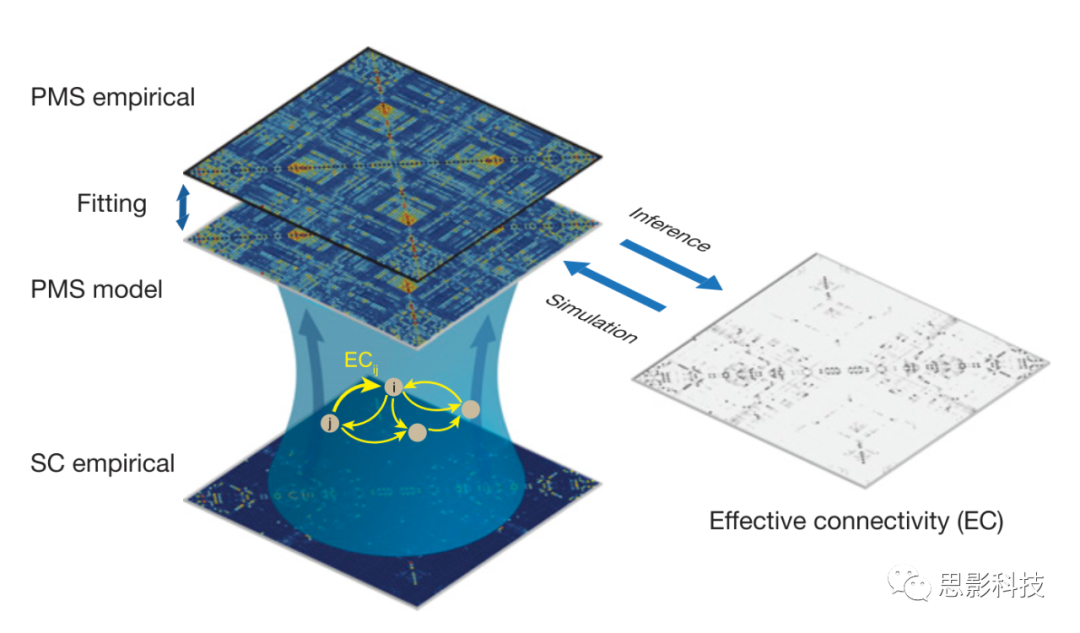
图4通过优化脑区之间突触连接的有效性[有效连接(EC)],证明了上述拟合程序是有改进的。具体来说,作者计算了模型与经验总平均相位相干矩阵之间的距离,并使用梯度下降法分别调整每个结构连接。该模型通过EC的递归更新重复运行,直到达到收敛。
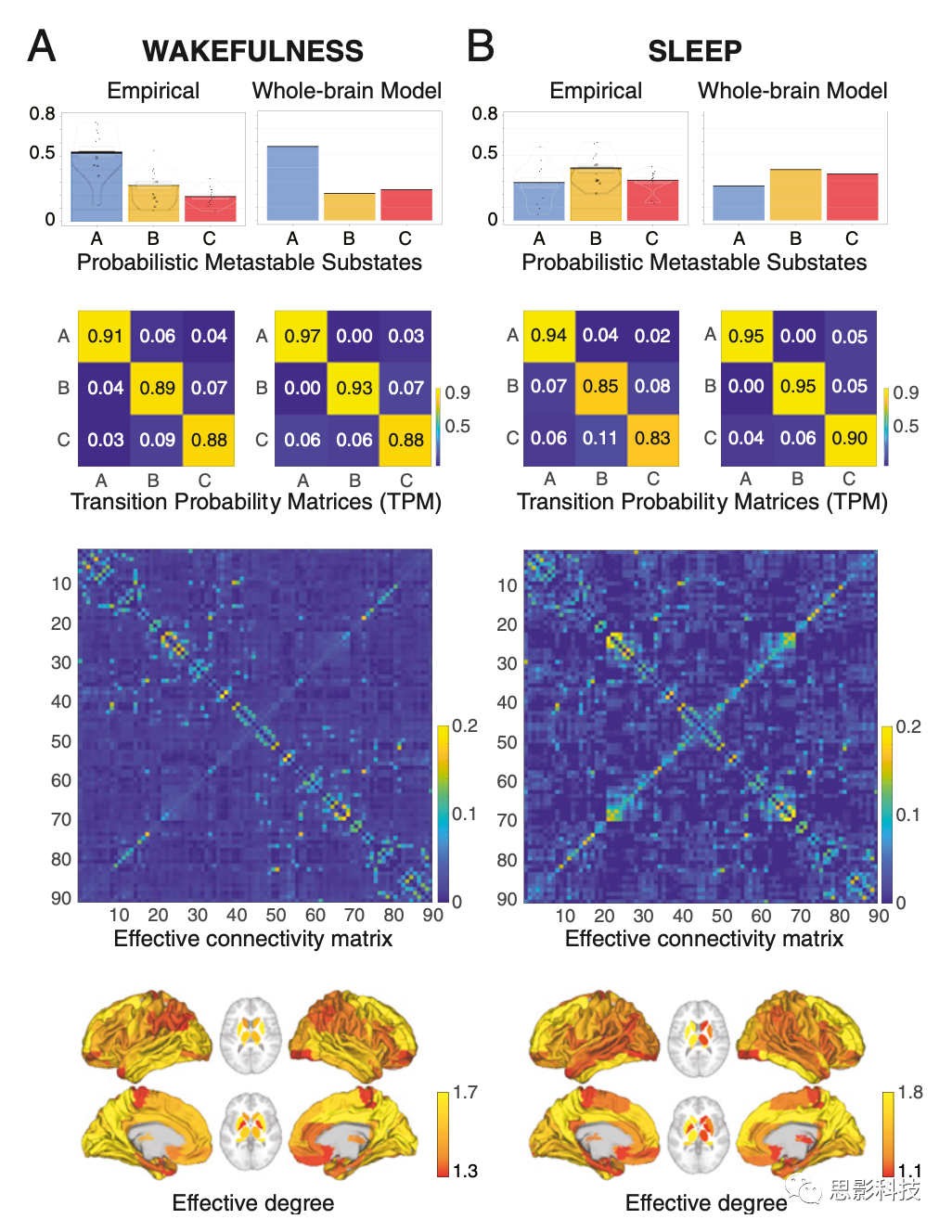
图5为清醒(图5A)和睡眠(图5B)时的结果,第一行为PMS空间,第二行为TPM(状态转移概率矩阵),左边一列为经验结果,右边一列为全脑模型的拟合。下面给出EC(有效连接)矩阵和有效度。在PMS空间的全脑模型拟合中,作者发现清醒状态的KL距离为0.0169,睡眠状态的KL距离为0.0045。同样,对于TPM(状态转移概率矩阵)的全脑拟合,作者发现清醒时的马尔可夫熵距离为0.098,睡眠时的马尔可夫熵距离为0.109。还要注意这两种状态下EC矩阵的不同。
![]()
图4. 使用有效连接(EC)连接全脑。
作者通过优化SC指定的脑区之间的突触连接的有效性,改进了拟合程序。作者计算模型与经验的平均相位相干矩阵之间的距离,并使用梯度下降的方法分别调整每个结构连接。该模型使用更新后的EC反复运行,直到收敛。
![]()
图5. 将一个全脑模型与使用fMRI测量的两种完全不同的大脑状态(清醒和睡眠)进行拟合。图中显示了清醒(左列A)和睡眠(右列B)的结果,并将经验结果与拟合的全脑EC模型的输出进行了比较。在每一行中,作者展示了PMS空间、转换概率矩阵、EC矩阵和有效度。可以看到,两种大脑状态的模型和经验数据之间有一个很好的拟合(例如比较PMS空间的条形图)。还请注意这两种状态的EC矩阵的不同程度。
![]()
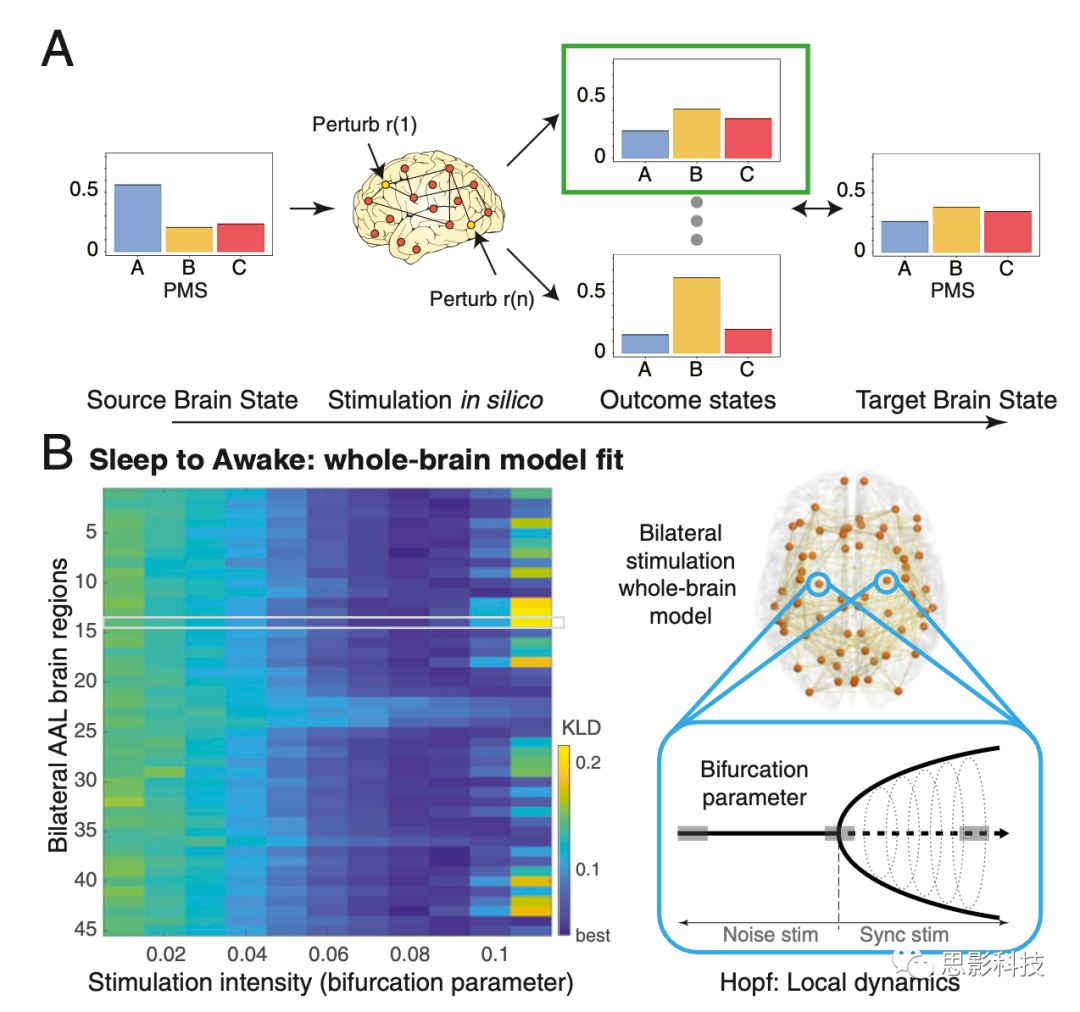
图6. 促使大脑源状态和目标状态之间转换的策略示意图。 (A) 可以系统地刺激源状态的全脑模型中的脑区,并将结果与目标状态进行比较。具体来说,在局部区域Hopf模型中,通过简单地改变分岔参数就很容易扰动模型。 (B) 刺激强度,即扰动的强度,与局部分岔参数的移动量直接相关。复合结果显示左侧刺激全脑EC模型。作者展示了在源状态(深度睡眠)中对不同刺激强度的45个脑区(使用双侧刺激)分别进行干扰时,大脑状态过渡拟合的KL距离。作者突出显示了一个灰色区域中的一个区域,它正在受到刺激,而其他区域则保持在其正常的分岔参数上。结果的颜色尺度显示了与目标状态(清醒状态)的拟合水平,即较低的值(深蓝)对应于最有效的转换。
唤醒:促使大脑状态转换。
之前的研究结果表明,作者可以成功地建立两个全脑模型,并与两种完全不同的大脑状态的经验fMRI数据非常吻合。然而,这项研究最重要的发现是它证明了通过外部刺激促使一个全脑模型向另一个全脑模型转换的可能性。
图6总结了促使大脑在两种状态之间转换的过程,作者系统地扰动源状态的全脑模型中的脑区,并将该模型得到的PMS空间与其他目标状态的经验数据进行比较(图6A)。具体来说,Hopf模型允许通过简单地改变给定脑区的分叉参数来扰动模型。刺激强度与局部分叉参数的偏移量直接相关(图6B,右)。作者在图6B(左)中对模型进行了双侧扰动,其中显示了目标状态(深度睡眠)中,分别扰动45个不同刺激强度的区域(因为是双侧刺激)时的大脑状态转换的拟合水平。图6 B(左)的颜色尺度显示了与目标状态(觉醒)的拟合程度,即较低的值(蓝色)对应有效转换。
对于主要的转换结果,作者使用了两种不同的协议进行外部刺激、同步和噪声,将局部分叉参数分别转换为正值和负值。图7A显示了使用同步协议(这里的协议是指固定的刺激参数和程序)促使从源状态(深度睡眠)转换到目标状态(觉醒)的结果,其中局部分叉参数的正值表示强制进行局部振荡,促进整个大脑更多同步的可能性。颜色刻度表示源状态和目标状态之间的KL距离,值越低表示拟合越好。当用足够的刺激强度扰乱大多数脑区时(a=0.08),这就促进了从深度睡眠到清醒的转换。在图7A中右边,作者展示了在这种刺激强度下促进转换的脑区的示意图。可以清楚地看出,虽然许多脑区能够促进转换(给予足够的刺激),但其他脑区不太适合促进这种转换(参见勃艮第地区)。重要的是在图7C中,作者表明使用噪音协议促使从深度睡眠转换到清醒状态是不可能的,刺激强度的增加导致KL距离更长,即较差的拟合,表明颜色从蓝色增加到更多的黄色。还要注意,图中的颜色比例是不同的。图7A和图7B与图中相比。图7C和图7D,每个图中的第一列具有相同的数值KL距离(对应于非扰动情况),但由于不同的颜色尺度而出现在不同的颜色上。
图7B显示了使用噪声协议促使源状态(觉醒)转换到目标状态(深度睡眠)的结果,其中局部分叉参数的负值会促使局部振荡,从而促进整个大脑出现更多噪声和更小同步的可能性。实验结果显示,清醒状态进入深度睡眠状态的特异性大于深度睡眠状态进入清醒状态的特异性,右图显示了脑区在刺激强度a=−0.4时促进状态转换的能力(注意勃艮第区域的增加)。重要的是,图7D显示使用同步协议在任何情况下都不会引起清醒到深度睡眠的转换(注意KL距离的增加)。这可以解释为促进从睡眠到清醒的转换可能比从清醒到睡眠的转换更容易。
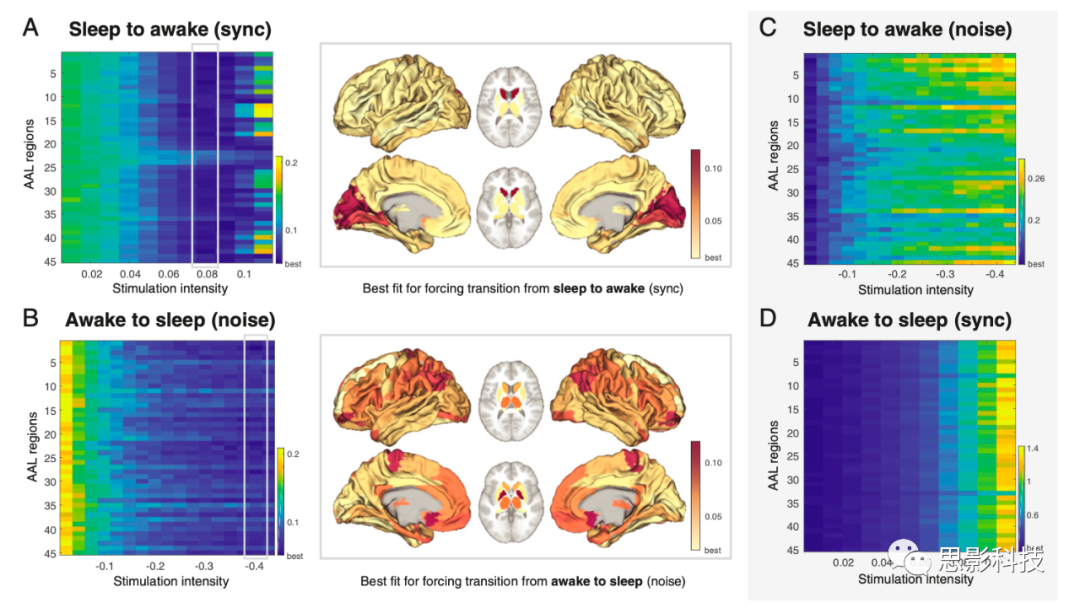
图7. 促使大脑状态之间转换的主要结果。
作者使用了两种不同的协议来进行外部刺激,即同步协议和噪声协议,它们分别将局部分叉参数移到正值和负值。
(A) 所示的是使用同步协议强促使源状态(深度睡眠)过渡到目标状态(清醒)的结果,其中局部分叉参数的正值迫使局部振荡,从而促进整个大脑中更多同步的可能性。颜色刻度表示源状态和目标状态之间的KL距离,较低的值表示更好的拟合(更多的蓝色)。可以看出,当以足够大的刺激强度干扰大多数脑区时,从深度睡眠到清醒的转换就得到了促进(a=0.08)。在右边作者展示了脑区在这种刺激强度下促进转换的能力。从结果中可以清楚地看出,虽然许多区域能够促进转换(给予足够的刺激),但其他区域不太适合促进转换(勃艮第区域)。
(B) 所示是使用噪声协议强迫从源状态(清醒)到目标状态(深度睡眠)的结果,其中局部分叉参数的负值迫使局部振荡,促进整个大脑更多噪声和更少同步的可能性。结果显示,使清醒的大脑进入深度睡眠的特异性比相反的大脑更强,右侧显示了大脑区域在a=−0.4的刺激强度下促进转换的能力(注意勃艮第区域的增加)。还请注意,噪声协议比同步协议需要更大的绝对值。
(C) 相比之下,转换并不总是可能的,例如当使用相反的协议来强制转换时。特别是,当使用噪声协议迫使从深度睡眠过渡到清醒时,刺激强度的增加会导致更高的KL距离,即更差的拟合,表明颜色从蓝色增加到更多的黄色。还要注意的是,A和C之间的颜色尺度不同,每个图中的第一列具有相同的数值KL距离(对应于非扰动情况),但由于不同的颜色尺度而出现在不同的颜色中。
(D)同样,当使用同步协议时,也不可能促使从清醒转向深度睡眠,如KL距离的增加即可表明。
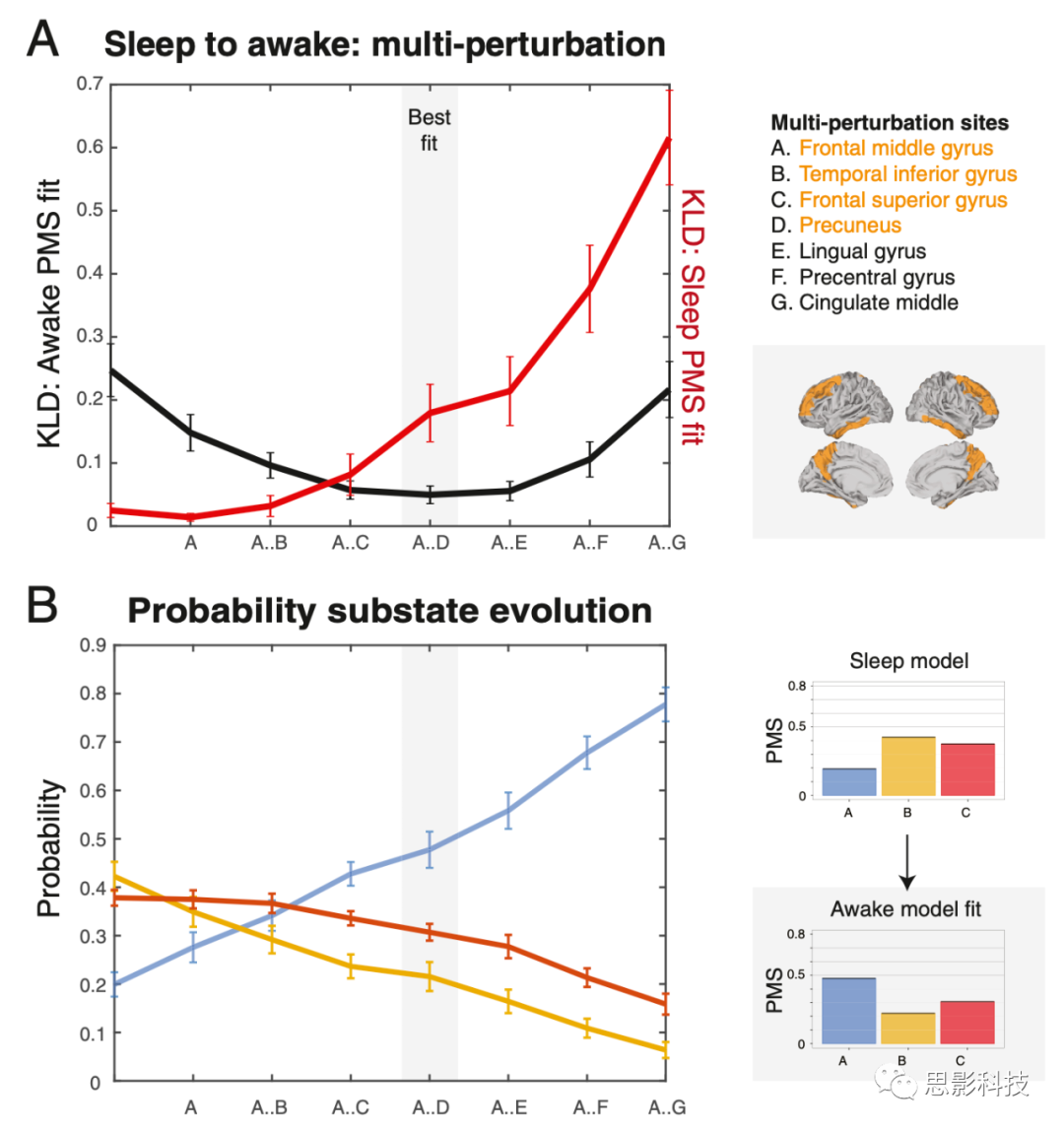
最后,作者探讨了刺激强度较弱的多个脑区是否会产生相同或更好的效果。图8显示了使用贪婪策略的多部位刺激协议的结果,以找到多个脑区的最佳组合,迫使状态之间进行转换(深度睡眠到觉醒)。使用同步协议,但在较弱的刺激强度(a=0.02)下,作者确定了最适合目标PMS空间的区域,并继续刺激该区域,同时在新条件下寻找其他区域中的最佳区域。该过程经过7个步骤的迭代。如图8A所示,多部位刺激的组合达到了其最佳拟合程度(与较高刺激强度下的单一部位刺激的最佳拟合程度相当,如图7A所示)使用4个双侧受刺激区域(额中回、颞下回、额上回和楔前叶),然后在增加更多区域后开始变差。黑线显示的是目标PMS空间(清醒)的拟合水平,达到4个区域的最小值。另一方面,红线表示与源PMS空间(深度睡眠)的拟合水平,并随着刺激部位的增加而变差。最后为了更好地理解多部位刺激如何促进转换,在图8B中,作者绘制了源状态(深度睡眠)和目标(觉醒)状态中3个子亚稳态的演化作为一个多区域刺激的功能。蓝线表示子亚稳态A的概率,随着受刺激区域的数量增加而增加,而橙线和红线表示子亚稳态B和子亚稳态C的概率降低。这很好地适应了PMS(亚稳态发生概率)在源状态和目标状态之间的转换,如图8B右边所示。
![]()
图8. 刺激强度较弱的多个区域的刺激可以产生与单点刺激相同或更好的结果。
作者使用了一个带有贪婪策略的多部位刺激协议来寻找多个脑区的最佳组合,以迫使状态之间的转换(深度睡眠到清醒)。使用同步协议,但在a=0.02的较弱刺激强度下,作者确定了最适合目标PMS空间的区域,并让该区域继续受刺激,同时作者寻找这个新条件下其他区域中的最佳区域。该过程重复了7个步骤。A图中显示了使用4个双侧刺激区域(在灰色阴影区域),多部位刺激的组合如何达到最佳拟合,然后在增加更多区域时开始变得更糟。最佳拟合值与较高刺激强度下的单点刺激的最佳拟合值相当(图7A)。这是用黑线表示对目标PMS空间的适合水平(清醒),并达到至少4个区域(用橙色区域标出)。相比之下,红线表示与源PMS空间(深度睡眠)的拟合水平,后者随着更多的刺激部位而变差。
(B)为了更好地理解多部位刺激是如何促进过渡的,图中绘制了源(深度睡眠)和目标(清醒)状态中的3个子亚稳态(蓝色、橙色和红色)作为多区域刺激的函数。黑线表示状态A的概率,它随着受刺激区域数量的增加而增加,而橙线和红线表示子亚稳态B和C的下降概率。这很好地拟合了源状态和目标状态概率之间的转换,如图所示,得到了相同4个区域的最佳拟合。
讨论
作者成功地使用全脑模型来拟合睡眠和清醒这两种截然不同的大脑状态的 PMS(亚稳态发生概率)空间。这些状态是根据健康被试在入睡期间采集的独特连续的神经影像,如fMRI和EEG等数据中提取的。作者表明这个全脑模型可以用来显示在哪里迫使不同大脑状态之间的转换,从而“唤醒”大脑使得状态从深度睡眠变为清醒,反之亦然。
作者旨在提供单个脑区促进这种转换时的证据,并且提供了原理证明,即多部位刺激可以以每个部位较少的刺激获得相似的结果。正如预期的那样,作者发现了一个最佳数量的区域,将促进状态之间的转换,而增加更多的区域将显著降低转换概率,反映了大脑状态的亚稳态性质。使用DBS等技术为大脑提供多部位刺激本身更加困难,但使用多焦tDCS阵列是可行的。然而,在这一点上,推测单点还是多部位刺激更最佳还为时过早。在正在进行的工作中,作者还证明了可以通过更多的生物物理现实模型来实现觉醒,如动态平均场模型,这说明了潜在的临床效益。
有趣的是,研究结果表明,唤醒该模型更容易,即睡眠到觉醒的转换更容易,而觉醒到睡眠的转换并不容易,在更多的区域需要更少的刺激。从进化论的角度来看这是有道理的,因为为了促进生存必须能够很容易地从睡眠中醒来,而容易入睡可能被视为不那么重要。
更广泛地说,这些结果必须在著名的拉丁命题“post hoc, ergo propter hoc”(“在此之后,因此如此”)的背景下才能看到,这是一个经典的逻辑谬论,混淆了相关性和时间序列与因果关系。长期以来,已经有许多引人注目的例子,在这些例子中,结果甚至可能先于原因,比如反向因果关系(例如,量子力学领域中的反向因果关系)。理查德.费曼(Richard Feynman)--F时钟和F门--理解所谓的复杂性高原(pos)的历史物理学家之一,即通过强制状态转换和描述与之相关的pos来理解复杂系统的物理状态。随着时间的推移,有一件事变得清楚起来:状态过渡在任何学科只能正确解释,预测,甚至成功执行,如果状态本身理解在必要的复杂性水平,和系统的自组织和动态可以建模,可能导致理论预测经验数据。
然而不言而喻的是,理解在类似大脑的系统中的状态及其动力学会使物理学似乎成为一个“简单”的物质。大脑的日常组织挑战了研究它的大多数努力,因为它的理解需要同时研究不同时空尺度上的局部和全球网络,以及它们随时间的动态进化。在宏观层面上,过去几十年来神经成像的发展已成为一个有价值的经验数据来源。
系统神经科学中状态的定义在当前受到极大的关注。以往研究尝试以许多不同的方式定义大脑状态,通常使用信号或信号组合的启发式定义,以及在一个经验定义的状态空间中描述给定时间大脑活动的点,通过定义相互作用的大脑区域的吸引子.其他方法使用全脑连接测量,包括dFC。然而,这些方法大多未能捕捉和利用各种限频神经生理信号的有趣作用和神经成像数据的时空丰富性。
作者描述的PMS空间策略捕获了异常大比例的数据,作为状态空间中的集合或概率“云”,这些数据可以分解为所谓的亚稳态,这些亚稳态是暂时稳定的,但作为时间的函数是可变的。在EC的基础上对模型进行微调并优化拟合。
使用这种数据约束的全脑模型的一个明显优势是它在研究刺激诱导的状态转换方面的潜在用途,因为它能够对所有潜在参数和位置进行详尽的搜索和优化,并可能最终为广泛网络的自组织提供见解。即使在实验动物或人类患者的大脑部位,这种见解也可能不被获得,因为DES已被证明违反了皮层微电路的最基本原理,通过沉默任何传入受到电刺激的新皮层区域的输出来破坏皮质--皮层信号的传播。例如,刺激外侧膝状体核(LGN)将产生在纹状皮层、丘和枕部中具有阳性BOLD反应的fMRI图谱,以及在所有纹状外区域中与LGN脱突触连接的负粗体反应。与fMRI同时进行的颅内记录一致证实,在刺激脉冲后立即发生的短兴奋性反应随后是长期的峰值抑制。这种抑制是突触的,而不是由于兴奋性的变化,因为注射GABA拮抗剂,如双亮氨酸,可以恢复刺激诱导的兴奋性反应。
人们早就知道,在皮层典型的微回路中,兴奋和抑制是密不可分的。感觉刺激将首先激发谷氨酸能神经元,约2毫秒后能激发GABA神经元。两者都有很强的周期性自扩增,微电路的输出取决于任何给定时间的所谓的激发-抑制(E-I)平衡。皮层传入的电刺激消除了E和I神经元之间的兴奋差异,同时激活两组,并通过上述强大的突触抑制和在反复自我放大开始之前分流微电路的输出。因此,在DES-fMRI实验中,猴子LGN的刺激划分了受刺激大脑部位的所有单突触靶点,或者通过反向刺激皮层内投射神经元侧脉到达的多突触核。因此,动物或人类中的DES通过皮质-皮质下-皮质途径传播,而不是皮质-皮质连接。通常不可预测的活动连接,以及作者仍然不能精确地定义由DES激活的元素。这就解释了大量帕金森患者遭受不良刺激效应的事实。理解刺激的状态和优化只能对未来尝试处理DES技术和解释其结果具有指导意义。
上述DES效应通过最大化可以由直接单突触或间接皮质下皮层路径激活的网络节点确实可以大大减轻患者的痛苦。
此外,该方法可以作为一种原则的方式重新平衡人类大脑活动健康和疾病因果改变亚稳态的云。此外,所提出的方法显着拓宽了先前同时神经影像活动和直接ON-OFF DBS 减轻脑疾病症状的全脑模型的发现,这些模型揭示了触发点和潜在的脑网络。例如,在计算机全脑模型中损伤和扰乱了大脑区域和网络,证明了大脑区域对人脑随着时间的推移有效整合信息的能力的因果贡献。
使用提议的框架,可以想象进一步的唤醒,甚至可能促进锁定患者的“唤醒”。一整套刺激技术,如DBS和TMS,可能会被用来推动健康与疾病之间的这种转变。然而现在也有可能使用靶向神经传递达到同样的效果,因为全脑模型已经成功地包含了神经传递。
总结:
总的来说,本文提出的方法和结果可以表征所有的大脑状态,包括意识水平、疾病和认知状态,这位大脑状态的量化定义作出了很好的尝试。同时,这样的量化方法是可能有很大的临床应用前景,因为它可以提供一种有原则的方法来发现如何迫使两种大脑状态之间的转换,并且模拟如何通过外部刺激来达成不同状态的切换。
如需原文及补充材料请添加思影科技微信:siyingyxf或18983979082获取,如对思影课程及服务感兴趣也可加此微信号咨询。另思影提供免费文献下载服务,如需要也可添加此微信号入群,原文也会在群里发布,如果我们的解读对您的研究有帮助,请给个转发支持以及右下角点击一下在看,是对思影科技的支持,感谢!

欢迎浏览思影的数据处理业务及课程介绍。(请直接点击下文文字即可浏览思影科技所有的课程,欢迎添加微信号siyingyxf或18983979082进行咨询,所有课程均开放报名,报名后我们会第一时间联系,并保留已报名学员名额):
核磁:
上海:
北京:
脑电及红外、眼动:
北京:
第六届脑电机器学习数据处理班(Python版,北京,3.31-4.5)
南京:
上海:
第三届脑电机器学习数据处理班(Matlab版,上海,5.15-20)
数据处理业务介绍: