在做决定时,人们倾向于选择看了更多的选项。注意力如何影响选择过程呢?乘法模型认为注视放大了被关注选项的主观价值;加法模型认为注视增加了一种恒定的、与价值无关的偏见。本研究使用来自多个实验室的6项实验数据验证了两种模型的拟和度。该文由俄亥俄州立大学的研究者完成,发表在期刊Psychological Science上。
研究方法:本研究检验了来自6项眼动研究的数据,以描述注视和选项价值在选择过程中的交互作用。其中2、3、4、6项研究采用EyeLink 1000 Plus眼动仪采集眼动数据。6项眼动研究数据均为二选一的数据集,其中数据集1-4是从两种食物中进行选择(食物选择任务),数据集5和6是从习得的符号刺激之间进行选择(概率任务)。在食物选择任务中(如图1a),每个试次的选项不同,也没有客观正确的选项。在概率任务中,选项会重复,有客观正确的选项,该选项获奖概率更高。在数据集5中(如图1b),共有6种不同的选项,对应30次选择。在数据集6中(如图1c),只有两对符号,每次选择时被试会看到其中一对符号。尽管这些符号在整个实验过程中保持不变,但每个符号产生奖励的概率随机变化。
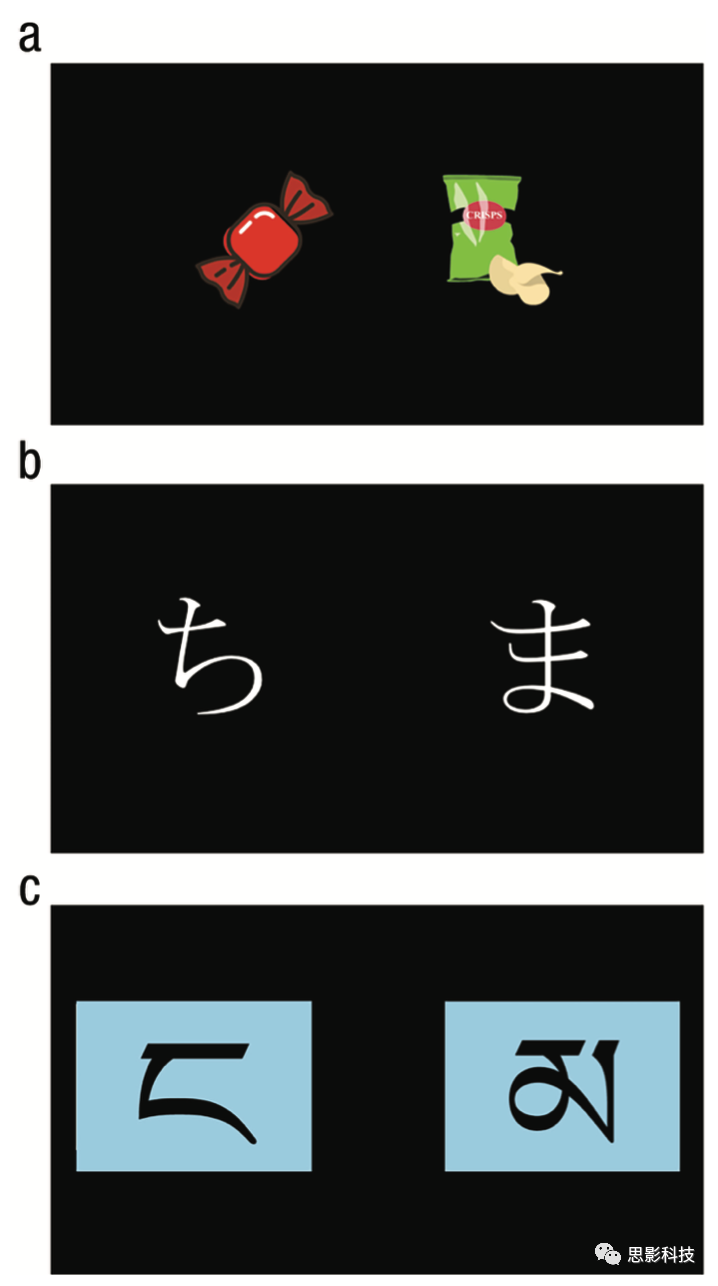
(Figure1)
六个数据集的特征见下表:
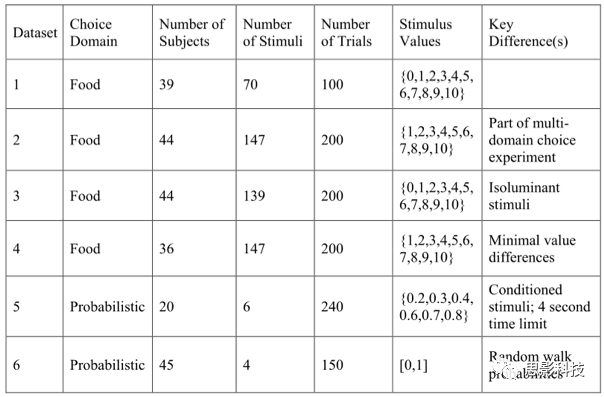
(Table 1)
模型计算
加法和乘法模型都依赖于顺序采样过程,通过该过程,选择中两个选项的相对证据得以积累。当支持一个选项的证据(相对于另一个)达到预定义的边界时,就会做出决定。证据积累的平均速率(漂移率ν)取决于两个选项的价值差异。这两个模型都假设漂移率随视线的每一次移动而变化。然而,模型在如何发生这种变化方面有所不同。乘法模型假设对一个选项的关注会导致在注视期间对另一个选择价值的折扣。加法模型假设对一个选项的关注只会短暂增加该选项被注意的证据。
乘法模型:
gaze left:ν= d(UL-θUR)gaze right:ν= d(θUL-UR)UL、UR 是左右选项的主观价值,d是价值的尺度参数,θ是注意折扣参数。
加法模型:
gaze left:ν= d(UL-UR+η)gaze right:ν= d(UL-UR-η)η—捕获注意力效应参数。乘法模型中具有较高价值的选项之间选择的漂移率变化剧烈,而加法模型的漂移率变化是常量。这个从两种模型的假设出发可以推论,乘法模型中由于注意折扣参数θ直接作用于不被注意的选项,导致其价值越大,变化就越大。而加法模型中的常量则对整体变化的影响比较稳定。如下图2所示:

(Figure 2)乘法模型和加法模型的图示(上为乘法模型)
模型验证:
(1)反应时(RT)与总体价值作者验证的第一个问题是,两个模型(乘法和加法)对备选项的总价值如何影响RT的预测。加法模型中的漂移率仅取决于选项间价值的差异,总体价值不影响决策。而乘法模型中,选项的总价值很重要,值越高,当视线从一个方向转移到另一个方向时,漂移率的变化越大,总价值大时会更快到达边界,从而缩短RT(见Figure 2)。为了验证该预测,本研究使用数据集2中的选择问题和Krajbich等人(2010)研究中获得的参数,用两个模型(乘法和加法)模拟了数据集,
并估计了以下回归模型:
log(RT)~β0+β1|UL−UR| + β2 (UL+UR).正如预期,乘法模型模拟了在RT和总值之间的负相关关系(图3a),而加法模型没有(图3b)。作者在6个数据集中都使用真实数据进行了拟合,在乘法模型模拟中,在每种情况下β2系数都显著为负,表明总值(UL+UR)的增加对应于RT的减少(图3c)。为了更直接地测试总价值和RT之间的关系,本研究进行了类似的混合效应回归,但只使用了值差等于零的试验。这使得模型可以放弃选项值差异变量,将模型简化为:log(RT)~β0+ β1 (UL+UR).结果发现在五分之四的数据集中,β1系数显著(见Table 2),证实了总价值和RT之间的负相关,为乘法模型提供了额外支持。
表2 总价值和RT的相关关系
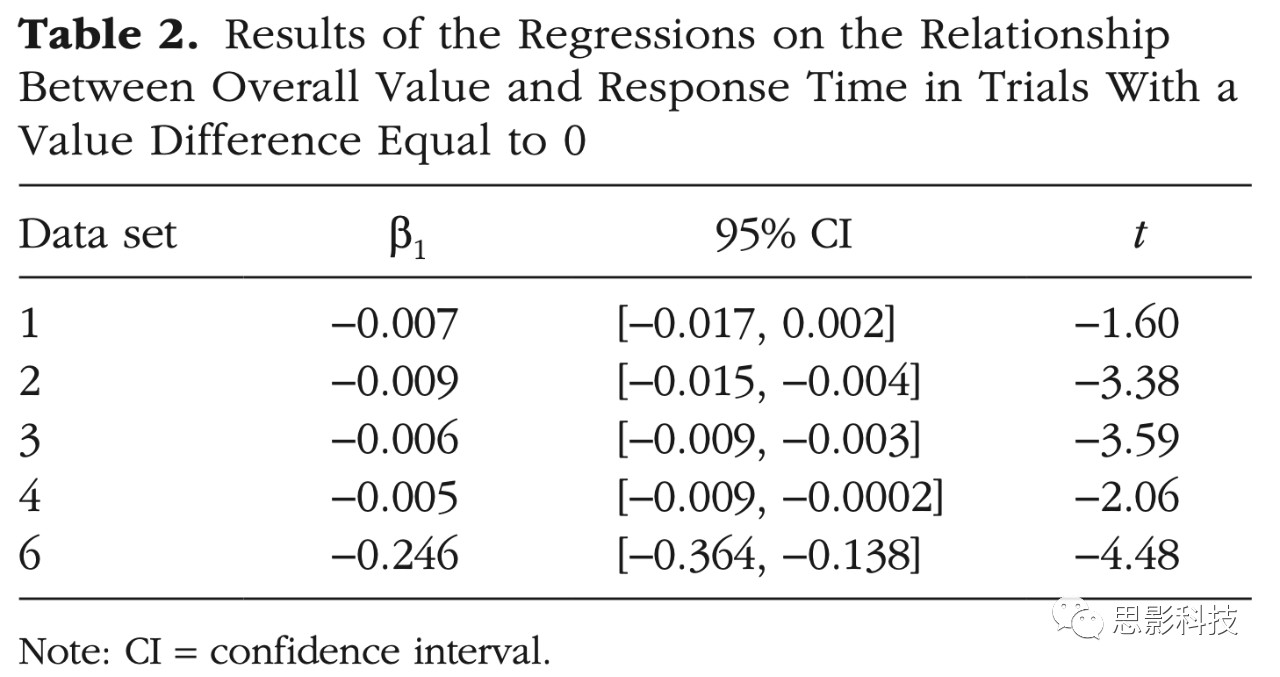
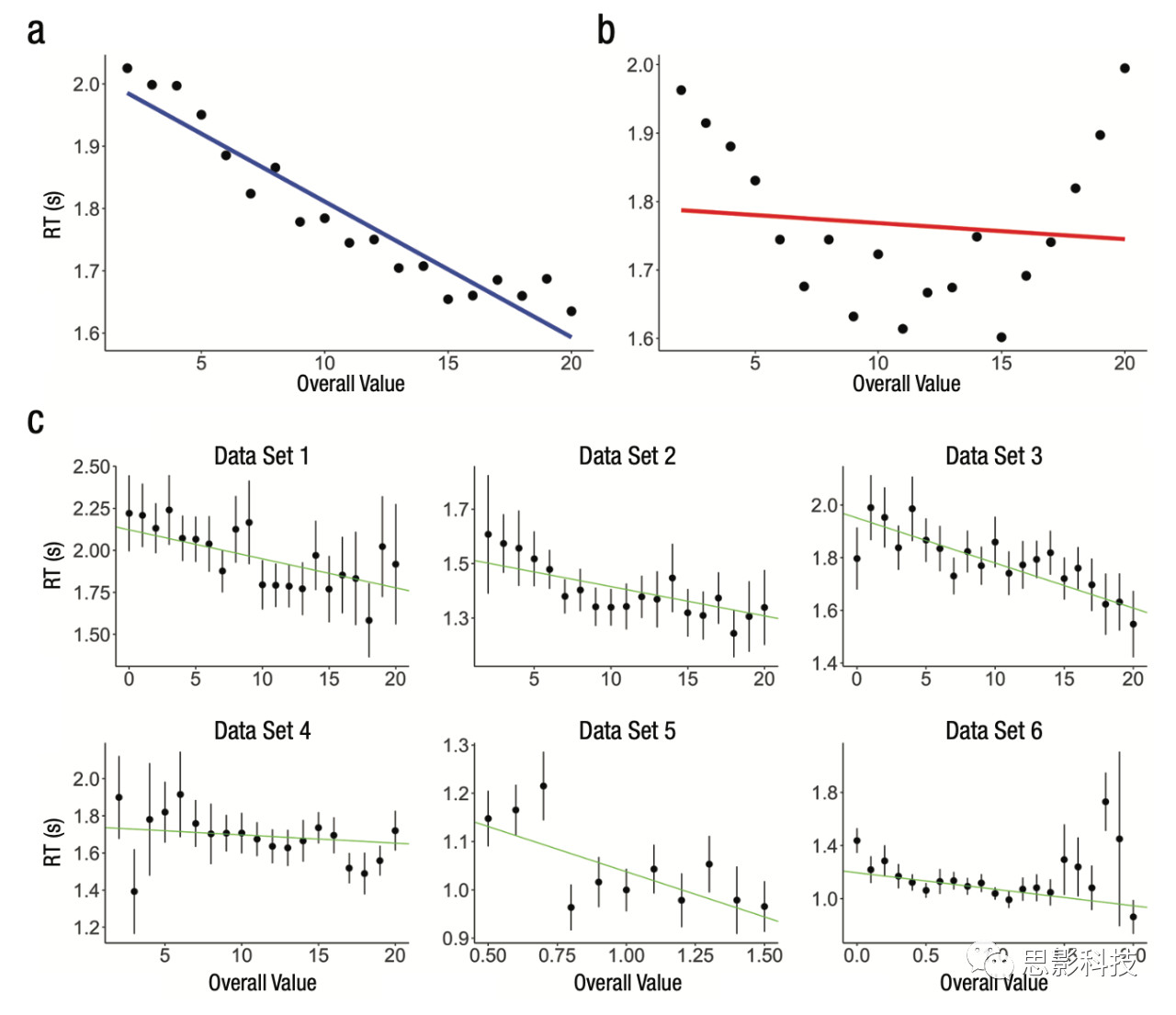
Figure 3 加法模型和乘法模型在数据集中的测试
(2)价值与注意力的交互建模
另一种测试注意力对选择影响机制的方法是建立价值和注视之间的交互模型。根据乘法模型,相对于关注价值较低的选项,关注价值较大的选项对选择的影响更大。而加法模型假定被关注选项的价值不影响注意力对选择的影响。为了验证这一预测,作者使用与之前相同的模拟和回归选择结果(选择左)对选项间的值差(UL− UR)、总值(UL + UR)和左停留比例(左侧选项的注视停留时间/总注视停留时间)进行分析,分为两种情况:一种是左侧值小于组数据集的中值,另一种是左侧值大于或等于组数据集的中值。换言之,在每次试验中,只有一个左停留比例变量具有非零值。更明确地说,其实是估计了以下的逻辑模型:choose left ~ β0 + β1(UL− UR) + β2 (UL + UR) + β3(left dwell proportion) |(left value < median (left value )) + β4 (left dwell proportion)|(left value ≥ median (left value)).然后,作者绘制了β3和β4的值(见图4a和4b)。如预期,乘法模型中低价值(β3 = 5.423)的左停留比例系数要小于高价值(β4= 7.029)。而加法模型对低价值(β3 = 5.750)和高价值(β4 = 5.757)具有相同的系数。这说明,乘法模型中对于左选择结果和价值比例之间的关系预测更加敏感。作者观察到,在6个数据集中的5个数据集中,高价值和低价值之间存在正性差异(见图4c)。各数据集的单尾配对样本t检验结果多为边缘或非显著。数据集1:t(37) = 1.99, p = .027;数据集2:t(43) =1.20, p = .119;数据集3:t(43) = 0.74, p = .233;数据集4:t(32) =−0.57,p = .713;数据集5:t(19) = 1.00,p = .166;数据集6:t(42) = 1.44, p = .079。然而,结合起来,发现在预期方向上有显著差异,t(221) = 2.25, p = .013。用中位数分割来估计注意力的影响,可以避免假设价值对停留比例和选择之间的关系有线性影响。作者也在每个数据集的单独级别运行了一个更简单的线性交互模型。分析结果支持在食物选择研究中的乘法效应,但不支持概率任务中的乘法效应。
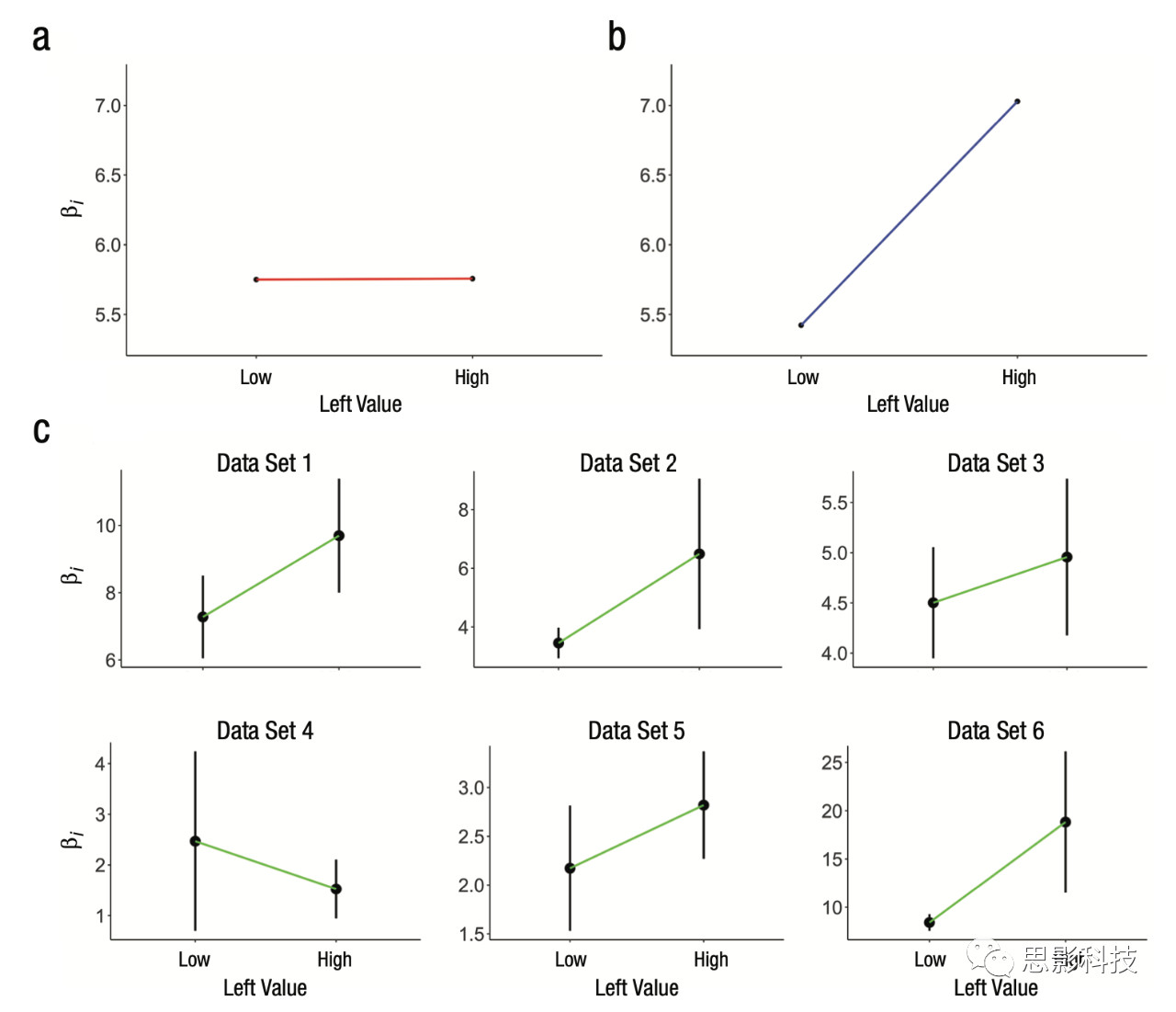
Figure 4 交互模型中对β3和β4参数的拟合
(3)模型结果
第一,计算RT与两个备选项总体价值之间的关系,发现较高的总体价值对应较短的RT。只有乘法模型可以预测这种关系。第二,研究注视停留时间对不同价值物品选择的影响,发现这种影响会随注视物品价值的增加而增加,尤其在食物选择任务中。这与乘法模型一致而与加法模型不一致。前面的分析强调了加法模型和乘法模型之间的关键区别,并指出了乘法模型的优势。然而,需要注意的是,这两个模型在其他方面提供了非常相似的拟合。为了了解这一点,作者使用加法和乘法模型分别来拟合所有数据集。两种模型都可以解释数据中的一些总体趋势。例如,两种模型都显示了反应时(图5b)和价值差异间(图5c)的反向关系,并且都捕获了被试选择他们所查看的最后一个选项的趋势。

图5 乘法模型和加法模型共同拟合的行为指标
根据整体拟合优度来比较模型是很自然的。然而,这样的比较可能取决于如何计算这些统计数据。即使使用标准的漂移扩散模型(DDM)拟合,也有各种各样的方法,在作者的研究中,希望考虑眼球跟踪的数据。一种方法是,作者根据被试是否最后看了选择的项目来调整数据,这种方法对两个模型产生了大致相同的适合度。另一种方法是根据停留时间差异来调整数据,这种方法更适合乘法模型。值得注意的是,在拟合过程中,这两种方法都没有对数据进行整体值的限定。除此以外,作者还测试了停留在左侧选项上的注意时间的持续时长和最终对左侧选项进行选择之间的关系。如补充图1所示,可以看出在6个数据集中有一致的证据表明对左侧选项的注意时间更长,其最终选择左侧选项的可能性就更高。

补充图1 停留时间与最终选择的关系
为了进一步研究注意与价值的相互作用,本研究使用了基于贝叶斯的分层模型(HDDM)评估了这两个。HDDM分析证实,数据集1-4支持乘法模型,贝叶斯后验概率分别为1、0.993、1、0.9885,但数据集5和6的结果是模棱两可的,数据集5中乘法效应的贝叶斯后验概率是0.391,数据集6中乘法效应的贝叶斯后验概率是0.025或1,这取决于在模型中使用的是主观值还是客观值。
研究结论:
数据结果支持乘法模型。具体而言,对某一特定选项的注视与该选项的价值相互作用,注视价值较高的选项比注视价值较低的选项对选择的影响更大。这种相关性在大量熟悉刺激的任务中比在少量习得刺激的任务中更明显。
总之,这项研究表明,注意力选择背后的机制并不是简单地增加被注视选项所积累的证据,而是考虑到选项的价值的更复杂的交互作用,特别是在来自大量熟悉刺激的选项时。
原文:Gaze Amplifies Value in Decision Making

微信扫码或者长按选择识别关注思影
第六届任务态fMRI专题班(重庆4.8-13)
第二十八届磁共振脑影像基础班(重庆2.24-29)
第十四届磁共振脑网络数据处理班(重庆3.18-23)
第二十九届磁共振脑影像基础班(南京3.15-20)