Current Biology：基于猴脑的神经电生理研究：神经回路抑制下的经济决策

 人们认为，商品之间的经济选择依赖于眶额皮层(OFC)，但对其决策机制仍知之甚少。为了阐明这个基本问题，作者记录了猴子在两种相继呈现的果汁之间的选择。对不同时间窗口的放电率的分析揭示了不同神经元群的存在，这些神经元群与之前在同步放电条件下发现的神经元群相似。这一结果表明，两种模式下的经济决策是在同一神经回路中形成的。然后作者研究了关于决策机制的几个假设。OFC神经元在基于果汁的表征(标签)中对果汁(identities)和价值(value)进行编码。与前人研究结果相反，作者的数据反驳了决策依赖于价值水平不同水平的相互抑制进行编码的观点。事实上，作者证明了对相互抑制机制的观察会被价值范围的差异所混淆。相反，决策似乎涉及回路抑制机制，即每个提供给猴子的价值（即文中的offer value）间接抑制了神经元编码使得猴子进行了相反的结果选择。作者的研究结果与之前的许多发现相一致，为经济选择的神经基础提供了一个大致的解释。该文章发表在杂志《Current Biology》上。

 

方法

实验设计、操作与记录

在实验过程中，让一只猴子坐在一个绝缘的笼子里，限制其头部活动。一个电脑显示器被放置在动物前面57厘米处。用1khz红外摄像机监测注视方向，估计空间分辨率为0.2^o。     

在每个session中，动物在两种标有A和B的果汁中进行选择。这两种果汁是按顺序提供的，数量不一。图2A和2B说明了任务设计。每个试次开始时，动物注视监视器的注视点（0.35^o的视角）。0.5秒后，两种果汁依次呈现在屏幕中央。每个offer都由一组彩色方块表示，其中颜色表示果汁类型，方块数表示果汁量。例如，在图2A所示的试验中，动物选择了两滴葡萄汁和六滴薄荷茶。在offer的同时，以注视点为中心呈现一个小的彩色圆圈（0.75^o的视角）。在零offer（0滴）的情况下，圆圈向动物表示相应果汁的是什么。动物在首次注视（0.5s）、提供(offer)1（0.7s）、提供间隔（0.5s）、提供2（0.7s）、等待时间（0.5s）和延迟时间（0.5-1s）中保持中央注视。延迟结束时，注视点消失（“go”信号）。该动物用扫视表示其选择，并在果汁输送前保持外周注视0.6s。中央注视的公差为2.5^o。

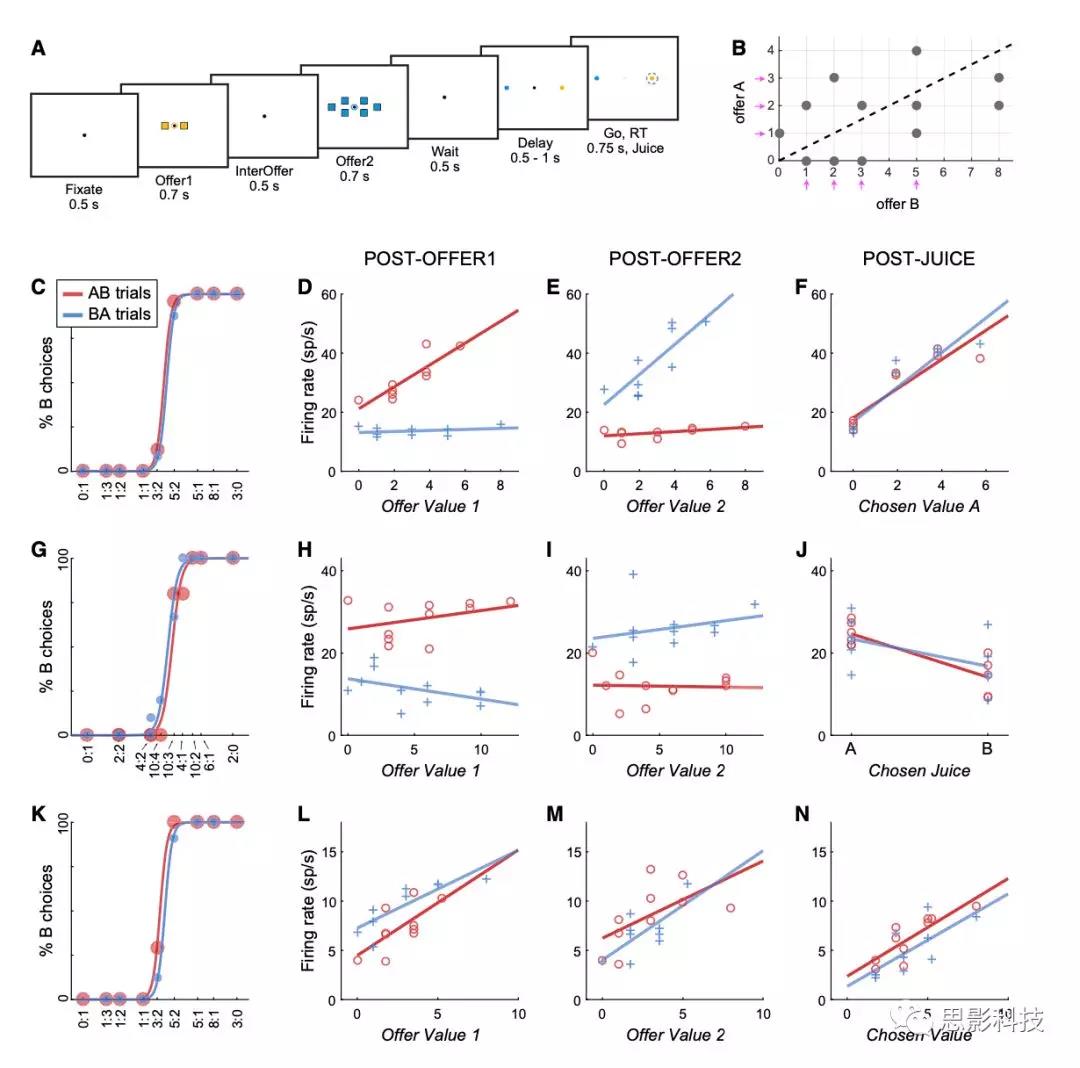
图2 实验设计和细胞样例

 

每个session包括300-800个trial，不同试次中，offer的数量不同(伪随机)(图2B)。对于每一对果汁量，呈现顺序(AB, BA)和扫视目标的空间位置是伪随机的，并在试次间进行平衡。在整个实验中，共使用了12种不同的果汁，果汁间的配对有多种可能性。果汁的种类和颜色之间的关系在整个实验中都是固定的。果汁量为70毫升至100毫升，在实验阶段内保持恒定。

实验共用两只动物(猴子J和猴子G)，每只动物在实验前都没有经过任务训练。在每只动物身上，作者都在全身麻醉下植入了一个头部限制装置和一个椭圆形的记录仪。腔体(主轴，50x30 mm)以立体定位坐标(A30, L0)为中心，长轴平行于冠状面。使用钨电极(直径100毫米;先进的定制电动系统驱动远程。电极通常成对排列(两个电极一个马达)，两个电极之间相距1毫米。使用10000倍放大器，滤波(高通截止，300hz;低通截止，6000Hz)并记录。在线检测动作电位，波形(40khz采样率)保存到磁盘进行离线分析。只有在整个过程中表现出良好隔离和稳定的细胞才被纳入分析。因此，该数据集包括来自猴子G的829个细胞和来自猴子J的438个细胞，共记录了209个session. 

选择模式分析

标签‘‘AB’’和‘‘BA’’反映呈现顺序(如，AB试次中先呈现A). 对于每个session，使用逻辑回归进行选择模式分析：

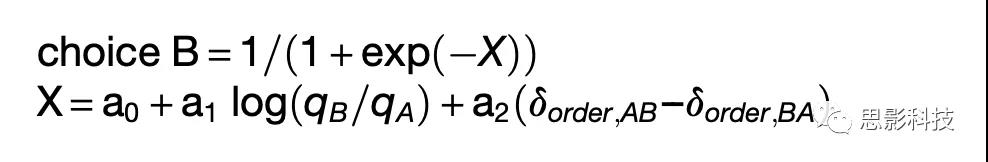
q_A , q_B 是提供给动物的A, B果汁的数量，在AB trials中δorder,AB= 1，在BA trials 中δ_order,AB = 0, 并且δ_order,BA = 1 – δ_order,AB. 拟合参数中, 作者推到出测量定义如下：果汁的相对价值ρ, η和ε:

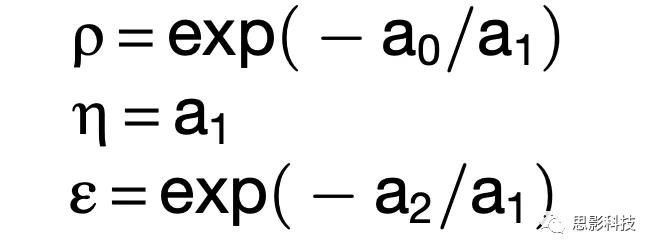
细胞分类

神经元数据的分析程序与前人在同时提供条件下的选择研究相似。每个细胞根据同一session中记录的选择模式进行分析。作者定义了8个与不同行为事件相关的0.5 s时间窗口:pre-offer(offer1之前0.5 s;控制时间窗)、post-offer1(offer1后0.1-0.6秒)、interoffer(offer2后0.4 - 0.1秒)、offer后(offer2后0.1-0.6秒)、offers off(offer2后0.6-1.1秒)、注视终止(从注视点消失前的0.1 s到消失后的0.4 s)、pre-juice(果汁呈现前0.4 s至呈现后0.1 s)、post-juice(果汁呈现后0.1-0.6 s)。一个“offer类型”是由给定顺序的两个果汁数量定义的(例如，[1A:3B]或[3B:1A]);“trial类型”由offer类型和选择定义(例如，[1A:3B, B]);“神经元反应”被定义为一个细胞在一个时间窗口内的活动作为trial类型的功能。

具体分析步骤如下：

Step1对数据进行方差分析(因素:trial类型)。至少在一个时间窗口内通过显著性阈值(p < 0.001)的神经元被确定为“任务相关”，并纳入后续分析。

Step2作者定义了大量OFC神经元可以编码的变量。其中包括一个二值变量表示顺序(AB | BA),八个变量表示个体的offer value(offervalue A, offer value A | AB, offer value A | BA, offer value B, offer value B |AB, offer value B | BA, offer value 1, offer value 2)，表示选择结果(选择果汁,选择顺序),选择价值(chosen value)的变量(选择价值,选择价值A,选择值B)以及价值差异的变量(valuediff (ch–oth); value diff (A–B); value diff (1–2))。分析中包含的18个变量定义在表S2中，图S7展示了变量之间的相关性。

对通过方差分析标准的每个反应在每个变量上进行回归。如果回归斜率与零显著不同（p<0.05），该变量可以“解释”该反应。在这种情况下，编码的符号（回归斜率>0或<0）。每个线性回归也提供了一个R²。当一个反应被多个变量解释时，变量的最大R²被认为是最适合反应的变量。而没有解释反应的变量，作者将R²设置为0。

表S2 方差分析结果

图S7 细胞分析中不同变量之间的相关矩阵

 

神经元通常在不同的时间窗口编码不同的变量。然而，对跨越时间窗口的神经元反应的初步观察表明，少量的可变序列可以解释种群中的很大一部分。因此，作者设置了多个时间窗口来检查神经元。具体来说，作者关注的是三种时间窗口，即post-offer1、post-offer2和post-juice。给定36个有符号变量和3个时间窗，就有46656个可能的序列。

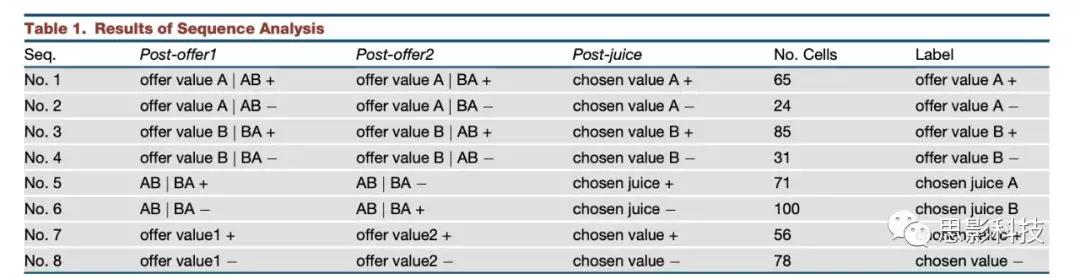
为了确定少数能最好地解释神经元群的序列，首先，对于每个神经元和每个序列，作者将“序列R²”定义为跨越时间窗口的和(R²)。如果序列R²>0，则称一个序列“解释”了一个细胞。对于每个神经元，作者确定了提供最佳解释的序列(最高序列R²)。其次，作者注意到相对较少的序列(N = 387)为≥1个细胞提供了最佳解释。为了对细胞数≥3及其镜像序列(通过翻转编码符号得到)提供最佳解释的序列，进一步将这个数字减少到N = 26(见表S3)。令k = 1,2,3…作者检查了k个序列的每个子集(>5×10⁶个可能的子集)。对于每个子集，作者通过将每个神经元分配到子集中的最佳序列，并将所有细胞的序列R²相加，从而计算出总R^2，从而确定了提供最大R²的最佳子集。

确定了8个序列的最佳子集后，将每个神经元分配给提供最高序列R²的序列。本分类结果见表1。

表1 序列分析结果

活动概况分析

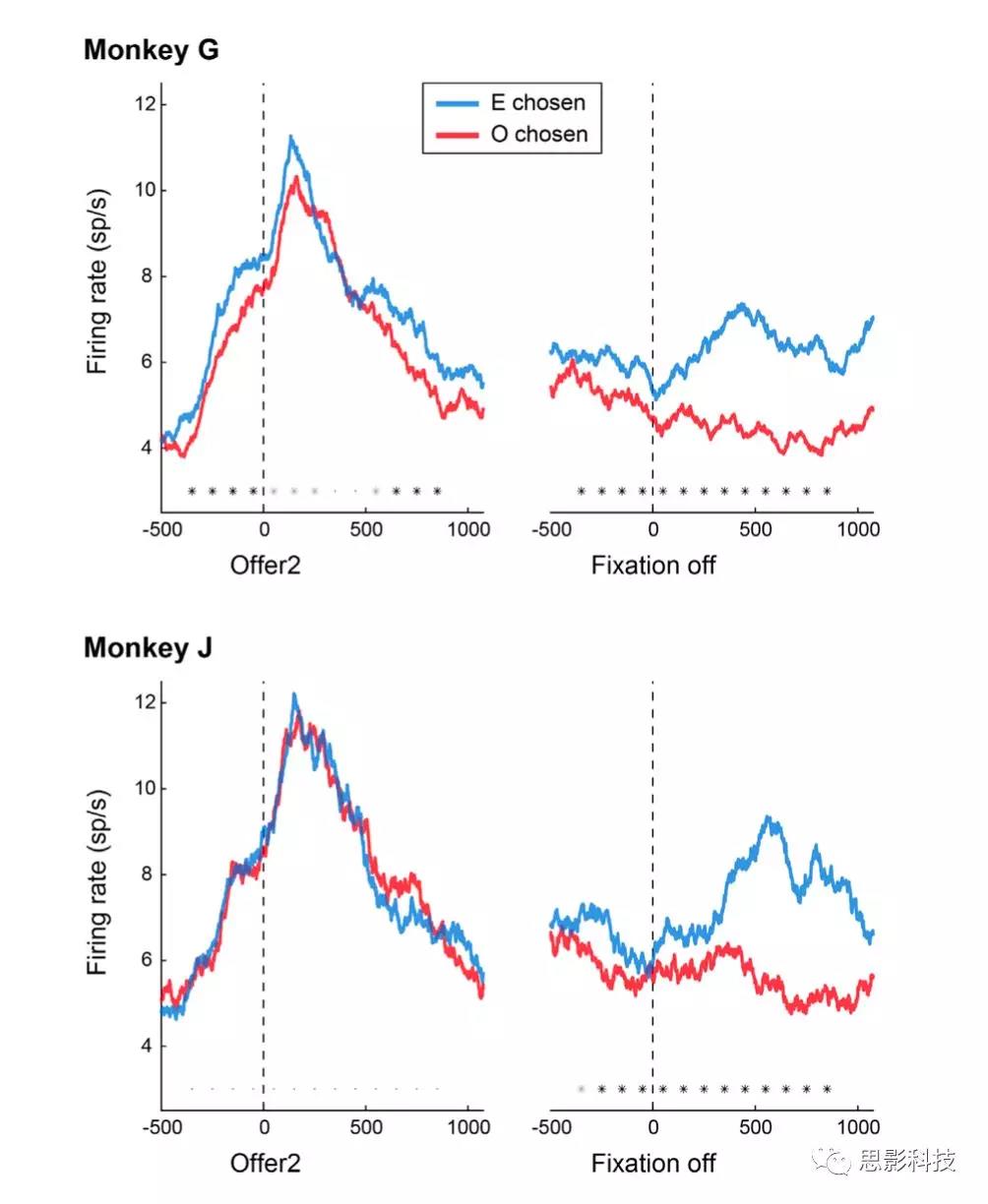
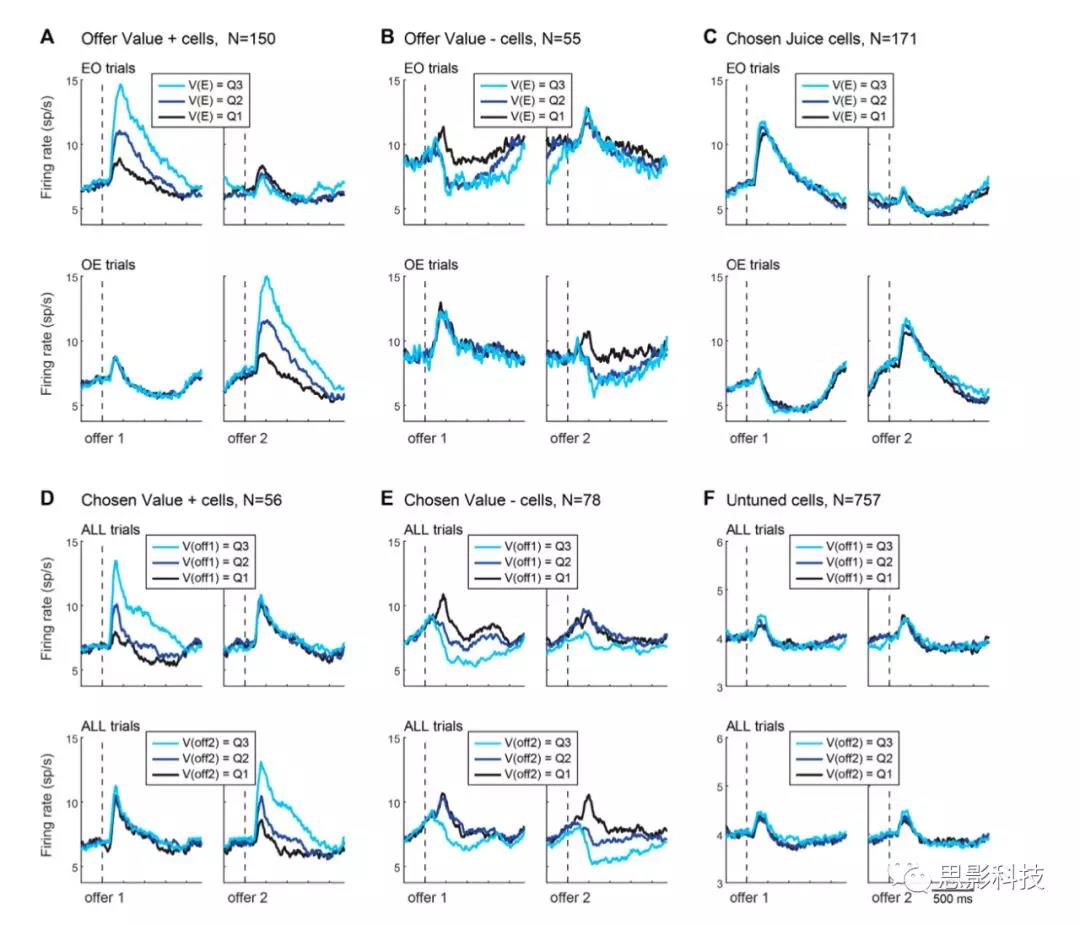
在确定了不同的神经元组之后，作者继续分析它们的活动情况。对于每个offer value细胞和每个chosen果汁细胞，作者将编码后的果汁标记为“E”，其他果汁标记为“O”(对于选择的果汁细胞，编码后的果汁会引发更高的放电率)。因此，对于每个细胞，根据果汁E是offer1还是offer2，分别以参考EO试次和OE试次作为参考。

为了计算活动概况，分别对offer1和offer2中的trial进行校准。对于每个trial，作者使用一个模拟突触后电位的核，通过施加时间上的影响(衰减时间常数= 20ms)来平滑动作电位的序列。在几次分析中，作者根据一些变量计算了特定神经元在三分位试次中的活动概况。为了做到这一点，将每个神经元的V(E)分布分成三等分，并在整个群体中对这三种活动进行平均。强迫选择被排除在这个分析之外。

用被试的ROC（特征曲线receiveroperating characteristic）分析chosen果汁细胞的活性。这个分析是0.5 s的时间窗上移动100 ms的数据得到的(图S6)。ROC分析的是原始的动作电位，没有经过平均及基线校正。对于每种offer类型，作者根据选择的果汁(E或O)来划分试次，并比较两种分布。对于每个时间窗口，ROC分析提供了曲线下的面积(AUC,area under the curve)，也称为选择概率。为了获得每个神经元的单个AUC，作者对offer类型的AUC取平均值。

图S6ROC分析

量化与统计分析

统计检验

统计检验包括方差分析、线性回归和简单t检验。方差分析是在单试次上进行的，这些数据通常具有Poisson分布。然而，这些分析仅用于识别与任务相关的细胞，采用了严格的标准（p<0.001）。因此，该方法是保守的。

简单的线性回归基于峰值个数在试次（神经反应）中取平均值（图S1），可以假设其近似正态分布。β系数的总体分析是使用Deming’s 回归法进行的，Deming’s 回归法考虑了两个轴上的误差，使用了从线性回归中得出的测量误差。从OFC和其他脑区记录神经元数据，关键分析集中在offer2后的时间窗上。神经元的反应被标准化，并根据变量offer value1和offer value2进行回归，每个项提供一个β系数。关键的发现是两个β系数呈负相关。β-反相关被认为是决策依赖于相互抑制的证据。在这里，作者证明这一结论是没有根据的，因为一个混淆因素，即价值范围不同而导致的差异。一旦控制了值范围的差异，β相关就消失了。因此，作者没有发现在offer水平上相互抑制的任何证据。

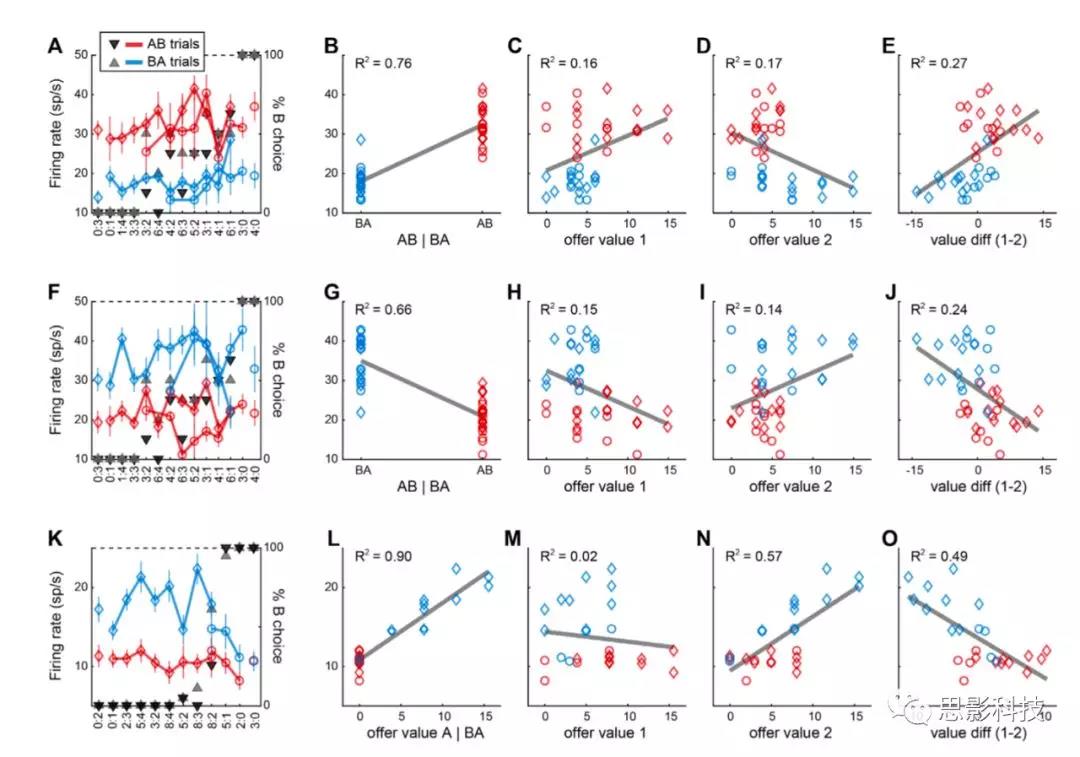
图S1 特殊值范围引起的beta反相关

 

Beta反相关并非意味着相互抑制

图S1A-S1E中的神经元反应几乎是二值化的，AB试次高，BA试次低。换句话说，这个响应编码了变量AB|BA（图S1B）。变量offer value1对应的神经元反应（图S1C）,由于AB试次和BA试次的动作电位激活数目不同，再加上数值范围的差异，所有数据点的线性回归均为正斜率（b1>0）。类似地，所有数据点与变量offer value2的线性回归发现负斜率（b2<0）（图S1D）。此类反映对变量AB|BA进行编码，但同一时间窗口中的其他反应使用相反的符号（变量-AB|BA）对果汁进行编码。此类反应中，对offer value1和offer value2的线性回归都将发现β₁<0，β₂>0。在总体分析中结合这两组反应，这些模式将导致β-反相关。

 Beta系数的神经元群分析

为了评估神经元群体中决策变量的编码，作者检查了在多个参考框架中定义的多个变量。因为，不这样做会导致错误的结论。无论决策机制如何，β-反相关可能是由多种因素引起的，如offer相关性或不相等的value范围。在作者的数据中，一旦假因素被控制，β系数不呈现任何正相关或负相关。因此，以前的研究结果很可能是由于价值范围的差异。 

结果

编码变量

作者记录了来自两个动物OFC的1267个细胞的活动。作者检查了与不同行为事件相关的8个0.5秒时间窗口的动作电位触发率。在8个时间窗口内，612/1267(48%)个细胞与任务相关(表S1)。将分析限制在3个主要时间窗口(post-offer1、post-offer2和post-juice)，538/1267(42%)细胞与任务相关。在第一次评估中，许多神经元似乎在AB和BA试次中呈现出不同的放电模式。例如，图2C和2D显示了一个细胞(post-offer1 时间窗口)相对于变量offer value1的活动。在AB试次中，细胞的激活率随着offer value的增加而增加(细胞似乎编码了offer value A)，相反，在BA试次中，细胞没有线性相关。这种情况很常见。然而，在两组试次中，失误率通常是相关的。例如，对于图2D中的细胞，BA试次中记录的放电率接近于果汁A的量为0时的预期值。换句话说，作者可以定义一个单一变量offer value A| AB (AB试次中的offer value A,BA试次中的offer value0)来解释整个神经元的反应。更正式地说，假设线性调谐，任何神经元的响应都可以写成：

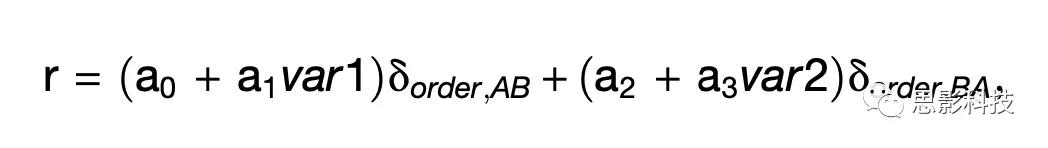
其中r为放电率，var1和var2为两个变量，如果oder = XY，则δ_order,_XY = 1，否则为0，a0…a3是回归系数。在一般情况下，var1和var2可以是任意两个变量和a0…a3是相互独立的。对于绝大多数的神经元反应，作者可以在两组试次中定义一个系数相同的单一变量，使方程简化为：

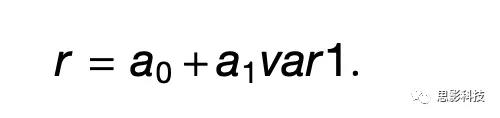
作者考虑了大量可以用OFC编码的变量，共分析了18个变量(表S2)。每个反应分别对每个变量进行回归。如果回归斜率与0有显著性差异(p < 0.05)，作者说变量解释了反应，作者关注斜率和R²。在1751个通过方差分析标准的反应中，1671个(95%)至少被18个变量中的一个解释了。图3提供了在不同时间窗口中编码的变量的总体情况。

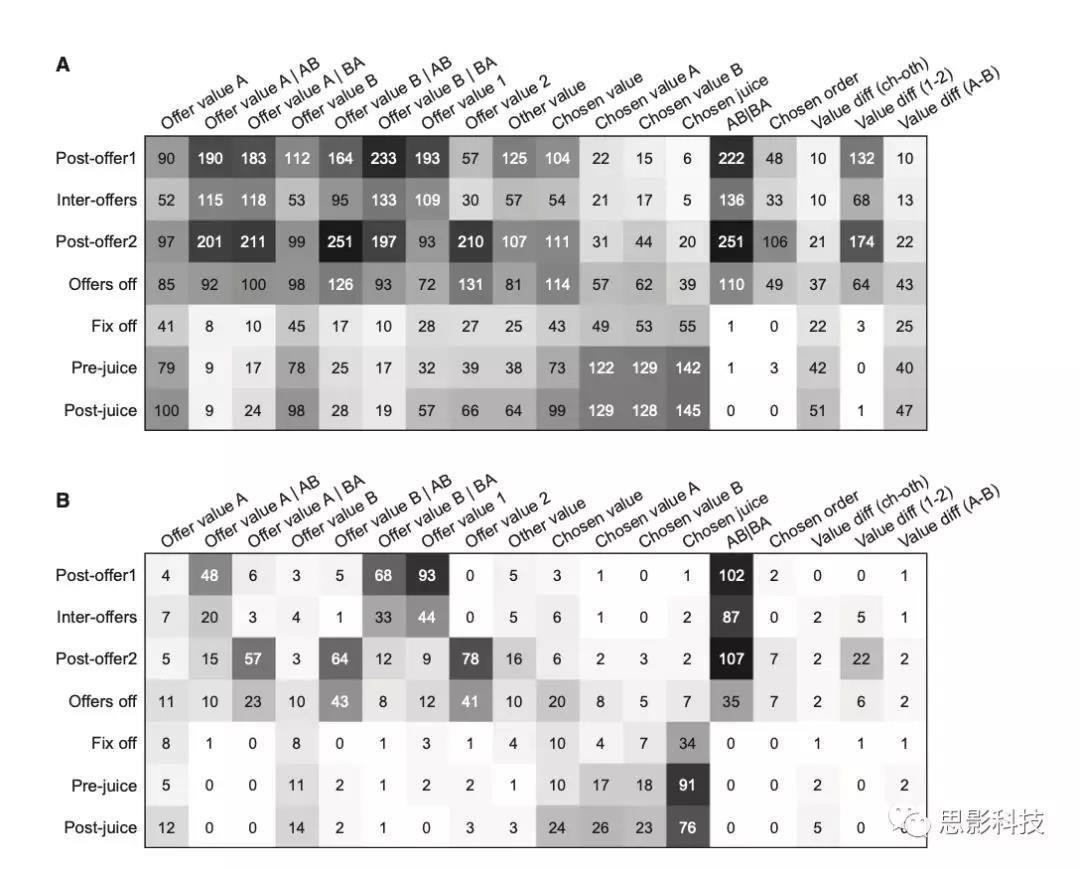
图3 编码变量及神经元群分析 

神经元分类

作者试图评估OFC神经元是否典型地跨时间窗编码相同的变量序列。对于这个分析，作者主要关注3个主要时间窗口(post-offer1, post-offer2, and post-juice)。考虑18个变量，2个编码符号，3个时间窗，有46656个可能的变量序列。作者的目标是评估一个小的序列子集是否可以解释整个数据集。原则上，作者可以对k = 1,2,3……序列的所有子集进行详尽的分析。对于每一个k，作者可以将最佳子集确定为解释能力最强的子集。不幸的是，有这么多可能的序列，穷举搜索是不可行的。然而，作者注意到至少对某些神经元提供最佳解释的序列相对较少。因此，作者集中研究了26个序列，它们最好地解释了至少3个细胞(表S3)。值得注意的是，作者发现8个序列的最佳子集解释了510/538(95%)的任务相关细胞(图4)。

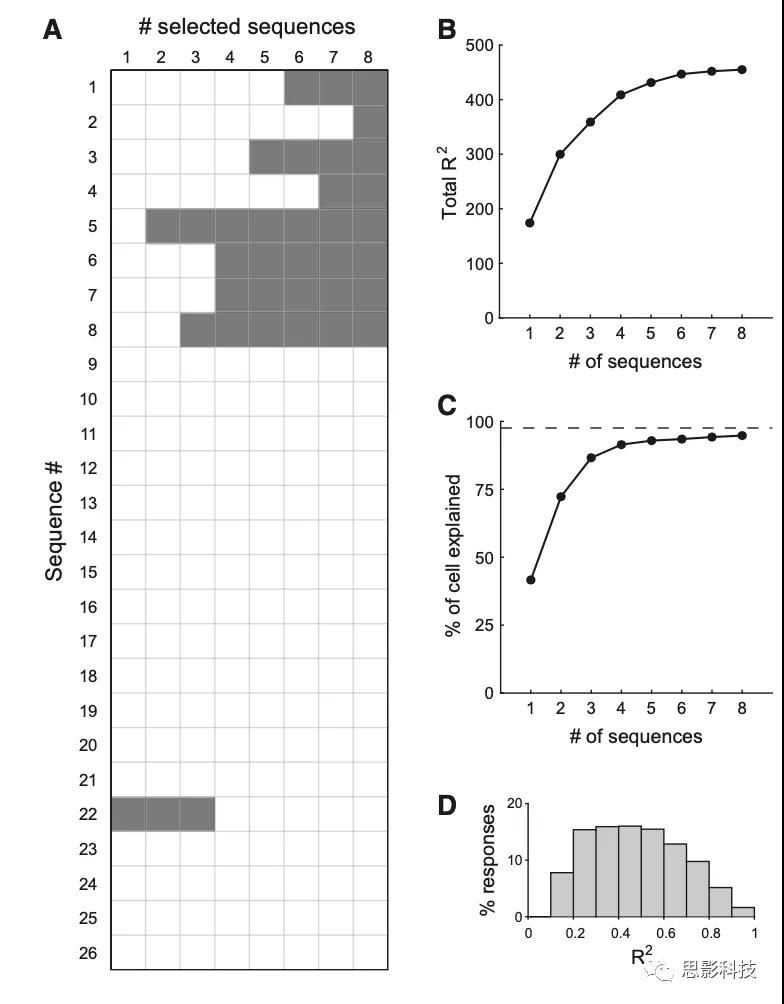
图4 序列选择分析

 

决策机制

假设1(H1): 单神经元池（single pool）

有人提出，顺序提供下的决策由单个神经元池处理，作为接受/拒绝决策的序列，与标签无关(图1E)。然而，正如上面所讨论的，在作者的数据集中，大多数(70%)与任务相关的细胞与特定的果汁有关，而与A或B(序列1-6)无关。此外，这些神经元对offer1和offer2的反应也不同。这些结果与单神经元池的假设不一致，并反应了标签意义的存在。

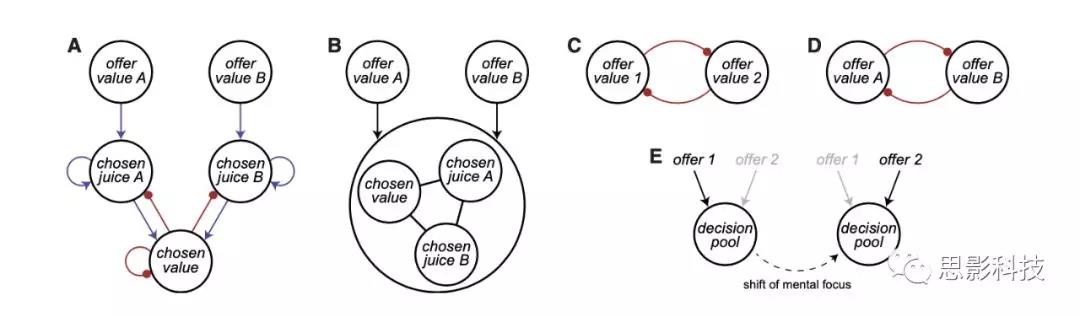
图1 决策模型

假设2 (H2):基于顺序的相互抑制

有几项研究考察了顺序提供条件下的决策，并提出决策是在offer value细胞水平上通过相互抑制而发生的(图1C)。在这些实验中，可供选择的物品有一些以视觉特征为代表的独特特征。例如，在一个选择任务中，两种奖励与不同颜色代表的不同奖励强度相关。分析主要集中在post-offer2的时间窗口。神经反应根据变量 offer value1和 offer value 2进行归一化和回归，每一项提供一个系数。关键的发现是，两个beta系数在神经元群中呈负相关。这一观察结果被作为证据，证明了在offer value水平上的决策依赖于相互抑制。然而，在这里，作者表明，该结论是没有根据的，因为beta反相关关系可能与决策机制无关（见上文）。在不相等的value范围的神经元中，作者发现了beta反相关，验证了以前的研究结果。然而，一旦控制了value范围的差异，beta系数就不存在任何正相关或负相关(图5)。因此，本研究不支持H2。

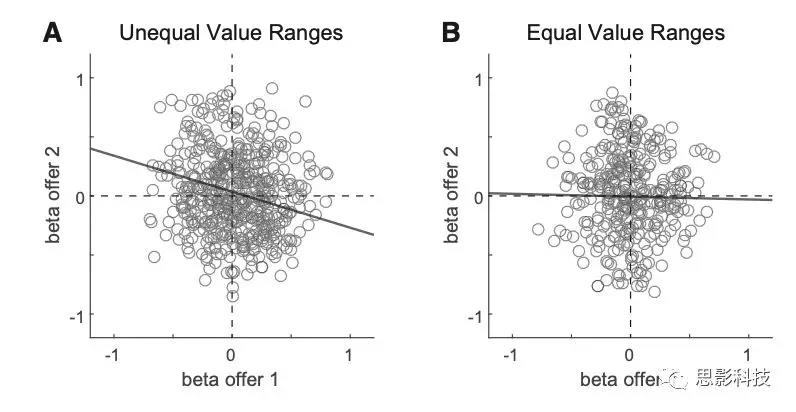
图5 在同value范围中的beta反相关解释

 

假设3 (H3): 基于果汁表征的相互抑制

原则上，决策可能需要与不同果汁类型相关的offer value细胞池相互抑制(图1D)。如果是这样，当决策发生时，直接参与决策的神经元的活动应该反映出两者offervalue之间的差异。与这一预测相反，这种神经元几乎不存在(1/1267;图3B)。对神经元活动的进一步分析证实了这一点。对于每个offer value细胞，作者将编码后的果汁标记为“E”，其他果汁标记为“O”。作者根据果汁E的value是低、中还是高将试次分为三组。H3认为，当果汁E呈现为offer2时，与果汁E呈现为offer1时相比(由于抑制作用)，offer value细胞对果汁E的反应应该降低。与这一预测相反，在offer1 (EO试验)和offer2 (OE试验)后记录的反应几乎相同，在统计学上难以区分(图6A)。对chosen value细胞进行的类似分析也得到了相似的结果(图6B)。

总之，作者的数据反驳了经济决策在offervalue水平上相互抑制的假设。

图6 活动概况和决策机制

工作记忆与回路抑制

在H1、H2或H3下，顺序提供的潜在决策的神经机制与同时提供下的潜在决策有根本的不同。另一种可能性是，这两种模式的决策是在同一个神经回路中形成的。如果是这样，对顺序提供下的选择进行分析可能会为决策回路提供强有力的见解。

当offer是连续的时，大脑必须保持关于offer value1的信息，并最终将其用于决策过程。目前的模型（图1A和1B）缺乏这种工作记忆功能，但可以对其进行修改，使之与工作记忆功能结合起来。在这个前提下，针对果汁A先提供的情况，一个合理的假设是，在offer1和offer2之间的延迟干预期间，offer value A细胞保持持续的活动。在offer 2 出现，决策在两个offer之间同时进行。然而，作者没有发现offer value1的任何持续活动编码（图6C）。对chosen value细胞的分析提供了类似的结果（图S4D和S4E）。这些结果表明，offer1的记忆痕迹可能分布在回路中或可能涉及其他脑区。

图S4 整个神经元群的活动概况s

 

作者研究了offer1的价值如何影响决策。作者的数据指出了一种回路抑制机制，即提供与一种果汁相关的value细胞，间接抑制与另一种果汁相关的chosen果汁细胞(图6D)。在这项分析中，作者把重点放在chosen果汁细胞上。对于每个神经元，激发更高(更低)放电率的神经元被标记为E (O)神经元。Chosen果汁细胞活性在offer1后不久呈上升趋势，然后下降。然而，在两个offer之间的延迟期间，活动逐渐增加，并被offer1的价值负调节。在offer2时，chosen果汁细胞的激发率与另一种未编码果汁的价值呈负相关(图6D)。图6A(左)和图6D所示的时间进程表明，chosen果汁细胞的抑制是间接的(回路抑制)。

图1A所示的神经网络为这种现象提供了一种可能的解释。在该模型中，offer value细胞和chosen果汁细胞分别是决策回路的输入层和输出层。这个决策是chosen果汁细胞的吸引力之间的竞争，由被chosen value细胞介导。这种竞争是由offer value细胞的输入和网络的初始条件决定的。

在这种解释中，回路抑制是决策过程的关键。如果是这样的话，chosen果汁细胞活动的随机波动应该是决策变量的一个来源。此外，chosen果汁细胞在offer2开始后的活动与决策结果的相关性应该越来越强。作者在OE试次中分析了chosen果汁细胞的活性。对于每个神经元，作者确定了动物不同选择中的offer类型，并通过ROC分析量化了动作电位活动和选择结果之间的关系(上文图S6)。

 

总结

经济决策需要回路抑制机制，即每个提供给猴子的价值（即文中的offer value）间接抑制了神经元编码使得猴子进行了相反的结果选择。作者的发现与基于联合抑制的神经网络模型相契合。

微信扫码或者长按选择识别关注思影