组水平的研究不能从网络结构上捕捉到个体差异，而网络结构是理解行为塑造的神经基质和开发临床干预措施的重要先决条件。最近的研究采用了功能连接的"指纹识别"分析来确定被试的特异性特征。在此，我们开发了一种以连边为中心的功能连接模型的补充方法，该模型关注于连边的共同波动。我们首先展示了相比于节点功能连接（nFC），全脑连边功能连接（eFC）是一个稳健的特征，eFC在不同的数据集和分区中的识别能力更强。随后，我们在不同空间尺度上，从单个节点到功能系统和集群水平（使用k-means聚类方法），描述了被试的识别能力（这里使用的k-means方法，是社区检测的常用方法）。在不同的空间尺度上，我们发现多模态脑区比单模态、感觉运动和边缘区域的脑区表现出一致更强的识别能力。最后，我们发现通过使用主成分的特定子集来重建eFC可以进一步提高识别能力。总之，我们的研究结果证明了以连边为中心的网络模型可用于捕捉有意义的个体特异性特征，并为今后使用eFC模型识别个体差异奠定了基础。本文发表在Neuroimage杂志。(可添加微信号siyingyxf或18983979082获取原文，另思影提供免费文献下载服务，如需要也可添加此微信号入群，原文也会在群里发布)。
可结合下文连边中心文章阅读，增进理解（思影可提供相关分析，如有需要请加微信siyingyxf或18983979082咨询）：
以连边为中心的人类大脑皮层功能网络揭示了重叠的系统层次结构
1 引言
在过去的几十年里，神经影像学领域已经利用强大的计算方法开发出了针对大脑形态和功能的标准化的群体层面的指标（Toga, Evans, 1998），增强了我们对认知、大脑发育以及神经精神疾病（Fornito等人，2015）的功能和神经解剖学基础的认识。然而，这些研究强调了组水平效应，而忽略了大脑组织的个性化和特异性。
最近，一些重要的研究已经开始将焦点从组水平分析转移到个体上（Dubois, Adolphs, 2016）。这一研究方向的目的是建立个体的大脑图谱（Joo, Boyd, et al, 2015），希望通过纳入个性化的细节来明确大脑组织、大脑-行为关系（Betzel, Satterthwaite, Gold, Bassett, 2017），并通过帮助设计更有效和更有针对性的干预措施，为神经精神疾病的治疗提供信息（Petersen, 2019）。
其中一个特别的研究方向是绘制大脑网络的特征，这些特征对个人来说是特异性的。就像指纹一样，这些特征能够区分一个人的大脑和另一个人的大脑。大脑网络指纹作为个体的可靠基础，具有较好的时间稳定性，跨FC数据子集（Byrge和Kennedy, 2019），以及跨采集地点（Bari等人，2019）。此外，识别特征已经显示出临床诊断的潜力（Svaldi等人，2019年），并被证明可用于个体行为和认知状态的分类（Salehi, Karbasi, Barron, Scheinost, Constable, 2020, Yoo, Rosenberg, Noble, Scheinost, Constable, Chun, 2019）。
迄今为止，大多数指纹分析都集中在来自大脑网络的特征上，其中节点代表定位电极（Cox等人，2018）或脑区（Amico，Goñi，2018，Finn，Shen，Scheinost，Rosenberg，Huang，Chun，Papademetris， Constable，2015）。最近，我们提出了另一种代替性的大脑连通性模型，它关注于网络连接（或连边）之间的互动性。我们把这些模式称为连边功能连接（eFC，连边功能连接关注的是两个连边之间的对话模式。可以分析对话模式的异同及其随时间的变化方式。强连边功能连接表明两个连边在时间上的共同波动具有很强的相似性，而弱连边功能连接则代表相对独立的共同波动模式）。采用以连边为中心的理念在其他科学学科中已经取得了丰硕的成果，如揭示复杂生物和社会网络的重叠社区结构（可以将社区理解为一类具有相同特性的节点的集合）（Ahn, Bagrow, Lehmann, 2010, Evans, Lambiotte, 2009）。最近的研究以"线图"形式使用以连边为中心的方法（Evans和Lambiotte，2009），用于区域间白质束的解剖学网络（de Reus等人，2014）。类似的，eFC为研究大脑组织提供了一个新的窗口，包括重叠的社区结构（Faskowitz等人，2020年）以及功能系统的参与在不同社区之间如何变化（Jo等人，2020年）。然而，关于eFC与传统的节点功能连接（nFC）在传递个体特定信息的能力方面如何，目前仍不清楚。
在此，我们应用一个新的以连边为中心的框架来探究个体识别中的脑功能网络。为了计算eFC，我们使用了一个和nFC类似的计算程序。首先对局部活动时间序列进行标准化（z-scoring）。nFC通常依据皮尔逊相关强度-两个标准化时间序列的元素乘积的时间平均值。在这里，我们省略了平均步骤，得到“连边时间序列”（Esfahlani, Jo, Faskowitz, Byrge, Kennedy, Sporns, Betzel, 2020, Sporns, Faskowitz, Teixera, Betzel, 2020）。连边时间序列的元素表示大脑区域节点（连边）对之间的瞬时共波动的幅度；当两个区域的活动在同一时刻向同一方向偏转时，共波动值为正，当活动在相反方向偏转时为负（当活动接近基线时为零）。为了计算eFC，我们计算成对的连边时间序列之间的相关性，从而形成一个逐边矩阵。直观地说，如果nFC反映了两个脑区之间的交流，连边时间序列代表了不同时间的交流模式，eFC代表了不同交流模式之间的相似性（Faskowitz, Esfahlani, Jo, Sporns, Betzel, 2020, Uddin, 2020）。
在本研究中，我们将基于功能连接的指纹识别扩展到以连边为中心的网络。利用来自两个独立获取的数据集（Midnight Scan Club（Gordon等人，2017）和Human Connectome Project（Van Essen等人，2013）；分别是MSC和HCP）的功能成像数据，我们比较了全脑nFC和eFC在个体识别上的表现，证明了在数据量充足的情况下，eFC比nFC具有更大、更稳健的识别能力。随后，我们从系统和节点水平，探究了提高eFC识别能力的驱动因素，使用基于节点的留一法关注系统的特异性。我们发现与多模态脑区系统相关的节点和连边是个体识别的主要驱动因素。最后，我们测试了是否有可能通过使用一组有限的主成分重建eFC和nFC来提高识别能力。我们发现在优化识别能力方面，重建后的eFC明显优于重建后的nFC。未来的研究可以利用eFC开发基于网络的生物标志物以追踪个体间在行为、发育和疾病诊断上的差异，我们的工作为此奠定了基础。
2 结果
在该研究中，我们系统地评估了eFC和nFC的差异识别能力，并讨论了它们在局部水平（节点）和子系统水平（节点组）的相似性和差异。在这一部分，我们分析了来自两个高质量的独立获取的数据集：the Midnight Scan Club（MSC；（Gordon, Laumann, Gilmore, Newbold,
Greene, Berg, Ortega, Hoyt-Drazen, Gratton, Sun, et al, 2017, Gratton, Laumann,
Nielsen, Greene, Gordon, Gilmore, Nelson, Coalson, Snyder, Schlaggar, et al.），其中包括10名参与者，每人扫描10次，以及来自Human
Connectome Project（HCP）的100名无关的被试，每人扫描2次。
2.1 使用连边功能连接计算识别能力
个体识别可以使用"差异识别能力"或Idiff进行量化，差异识别的计算方式为使用连接矩阵的平均个体内相似度减去平均个体间相似度（Amico和Goñi，2018b）。现有的个体识别应用依赖于来自nFC的连接模式，因此eFC的特异性特征仍然未知。在本节中，我们对比了大脑皮层nFC和eFC的识别能力及其对可用数据量的依赖性。
首先，我们比较了大脑皮层范围内eFC和nFC的识别能力。简而言之，这需要对MSC数据集中的100次静息态fMRI扫描数据（10个被试；每人10次扫描）单独估计nFC和eFC，并为每个连接模式生成相似性矩阵，作为被试nFC或eFC矩阵的上三角元素之间的皮尔逊相关性（图1e）。然后我们从这些相似性矩阵中估计出不同的识别能力（图1f）。
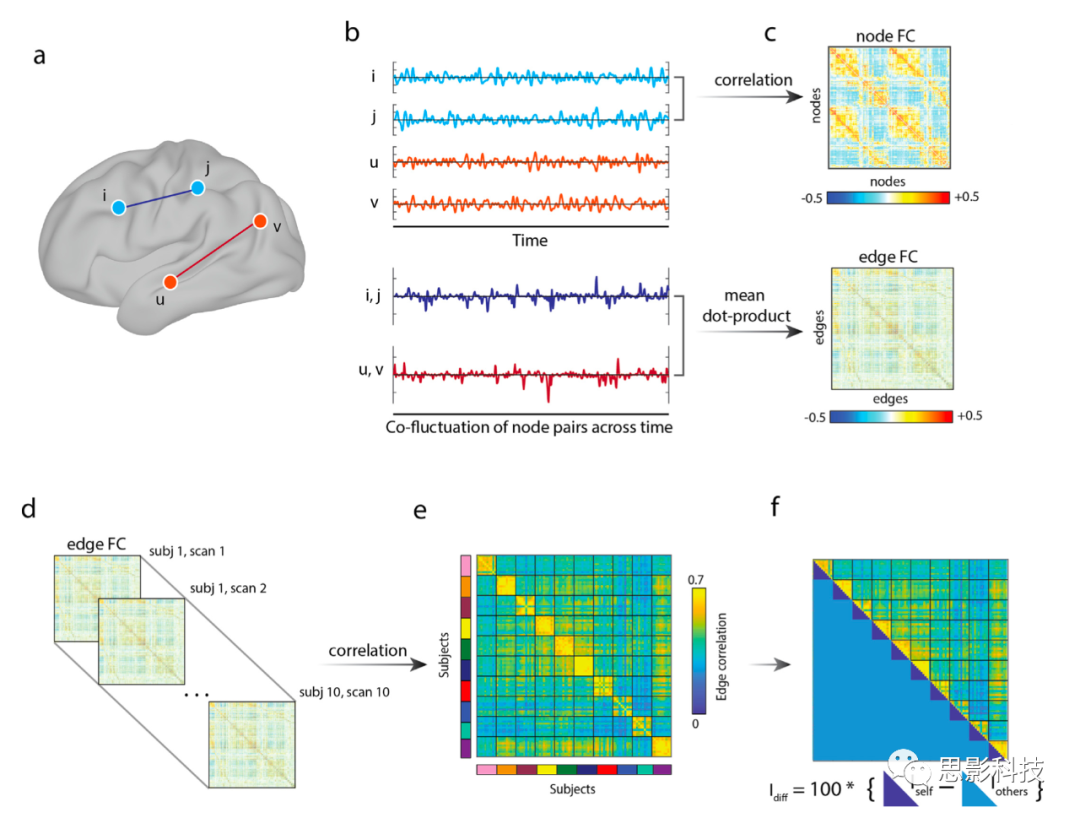
此图都是使用来自MSC数据集的数据生成的。
(a)为了说明节点和连边FC（分别为nFC和eFC）的计算过程，考虑四个节点：i、j、u、v。nFC被定义为局部活动的成对相关性。对于节点i和j，nFC通常是通过标准化(z-scoring)来计算每个时间序列，执行时间序列对的点积并计算乘积时间序列的平均值（b和c）。同样的操作可以应用到节点u和v。
eFC的计算过程为：首先计算z-scoring时间序列的点积，形成一组新的时间序列，其元素表示大脑区域对之间的瞬时共波动的幅度，但省略了平均步骤。
（b）。每个共波动时间序列即是一对节点定义的。eFC被计算为一对共波动时间序列的时间相似性（如相关性、余弦相似性等）
（c）。(d)为了计算差异识别能力，(e)我们提取了被试eFC矩阵的上三角元素，并计算这些元素的空间相关性，从而得到逐个被试间的相似性矩阵。
(f)差异识别能力或Idiff的计算方法是将被试内平均相似度减去被试间平均相似度。
我们发现当使用来自整个大脑皮层的功能网络时，eFC的表现优于nFC，出现了更大的Idiff（图2a）。在使用不同的分区和同一个独立数据集时也发现了类似的结果（图S1）。为了使被试内和被试间的相似性可视化，我们使用多维尺度分析将被试和他们的扫描图像投射到一个二维空间，该空间大致保留了nFC和eFC相似性矩阵中编码的成对距离关系（图2c-d）。因此，MDS图上两个扫描之间的距离代表着通过非线性降维测量的相似度。我们使用标准化的欧氏距离来计算每个扫描的被试标签与k-近邻的被试标签的准确性。我们发现使用nFC和eFC计算的平均准确率没有明显差异（t – test, p =
0.9786）。被试标签的准确性被计算为MDS空间中九个最近的点中与扫描的被试标签相匹配的被试的百分比。
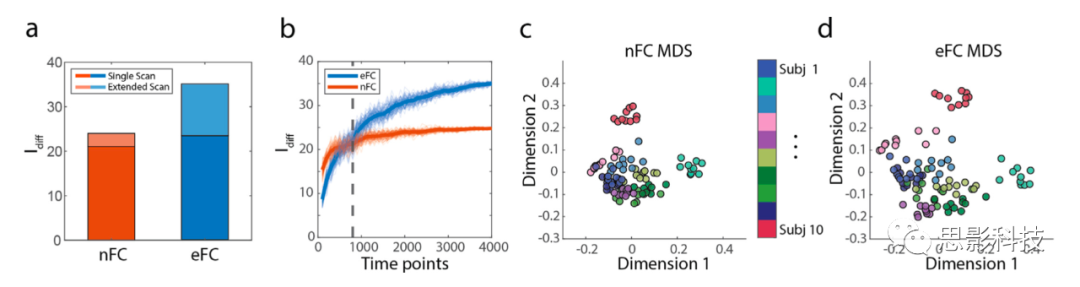
图2.eFC和nFC的个体识别和扫描长度的影响。该图使用来自MSC数据集的数据生成，包含有200个节点的Schaefer分区。
(a)单次扫描的（深色）和最大程度的联合扫描（浅色）nFC和eFC的Idiff。
(b)按扫描长度计算的eFC和nFC的Idiff。黑色虚线（800个时间点）表示eFC明显优于nFC的时间序列的长度。蓝色和橙色的粗线是100次迭代的平均Idiff，细线表示按扫描长度每次迭代的Idiff。
(c)使用多维尺度分析绘制了被试的nFC扫描图。
(d)使用多维尺度分析绘制了被试的eFC扫描图。每个被试的扫描结果分别对应于c-d之间色带上的一种颜色。
在前面的分析中，我们使用大约30分钟的数据（MSC数据集中的session的持续时间）计算eFC和nFC。随后，我们测试了个体识别能力是否受扫描长度的调节，即Idiff是否随着可用数据量变化（Amico, Goñi, 2018, Bari, Amico, Vike, Talavage, Goñi, 2019）。为了测试这一点，我们创建了更短或更长的session，将现有的扫描分为更短且连续的片段，或者将多个扫描的数据连接起来以形成更长的session。我们以100个样本的增量来改变人工扫描session的时间，从100开始到4000结束。整个取样过程重复了100次。我们发现，在少于500个时间点（约20分钟）时，nFC的Idiff比eFC大（p < 10-6，t - test）；图2a。然而,在800个时间点（约30分钟）开始，eFC明显优于nFC（p < 10-4;t - test）；图2b。我们使用不同的分区和数据集报告了类似的结果（图S1）。我们使用eFC的结果与以前的研究是一致的，即使用传统的nFC，识别能力随着扫描长度的增加而增加（Amico, Goñi, 2018, Bari, Amico, Vike, Talavage, Goñi, 2019）。总的来说，我们的研究结果表明只要有足够的数据量（大约30分钟），即使在不同的session，eFC比nFC更稳健地识别不同被试。
2.2 大脑皮层eFC识别能力的局部驱动因素
在上一节中，我们发现在有足够数量的样本的情况下，eFC比nFC提高了整个大脑皮层的识别能力。本节我们想找出对这一改进作出贡献的大脑区域。我们使用了节点留一法来衡量每个大脑区域对个体识别能力的相对影响。然后，为了对结果进行总结，我们根据典型的大脑系统对节点进行分组，并从统计学角度评估每个系统对整体识别能力的贡献。eFC测量成对的连边之间的相互作用，每个连边都对应一对大脑区域。为了确定哪些脑区驱动了这些效应，我们迭代地删除了200个脑区中的每一个脑区，并使用剩余的199个脑区重新计算eFC和Idiff。然后我们将这个Idiff值与使用完整大脑（所有200个区域）获得的值进行比较。这里，脑区是根据功能图谱（Schaefer等人，2017年）定义的。我们还用连边代替节点进行了类似的分析，其结果见图S2。我们发现当删除位于控制和颞顶网络区域的皮质区域导致了差异识别能力的降低，而删除与躯体运动、边缘和视觉网络相关脑区则增加了识别能力（图3a；为了可视化，我们将ΔIdiff的符号反转）。根据系统对所有节点进行分组，可视化每个节点对个体识别能力的贡献（图3b）。每个节点的贡献被衡量为没有一个特定的节点的Idiff减去所有200个节点的Idiff值。例如，在图3b中，在构建eFC之前，从控制A系统中删除一个节点（用一个黄点表示），将导致Idiff减少，我们认为这对Idiff有正向影响。相比之下，从边缘系统中移除一个节点会导致Idiff增加，因此我们认为这对Idiff有负面影响。
图3.节点对eFC中识别能力的贡献。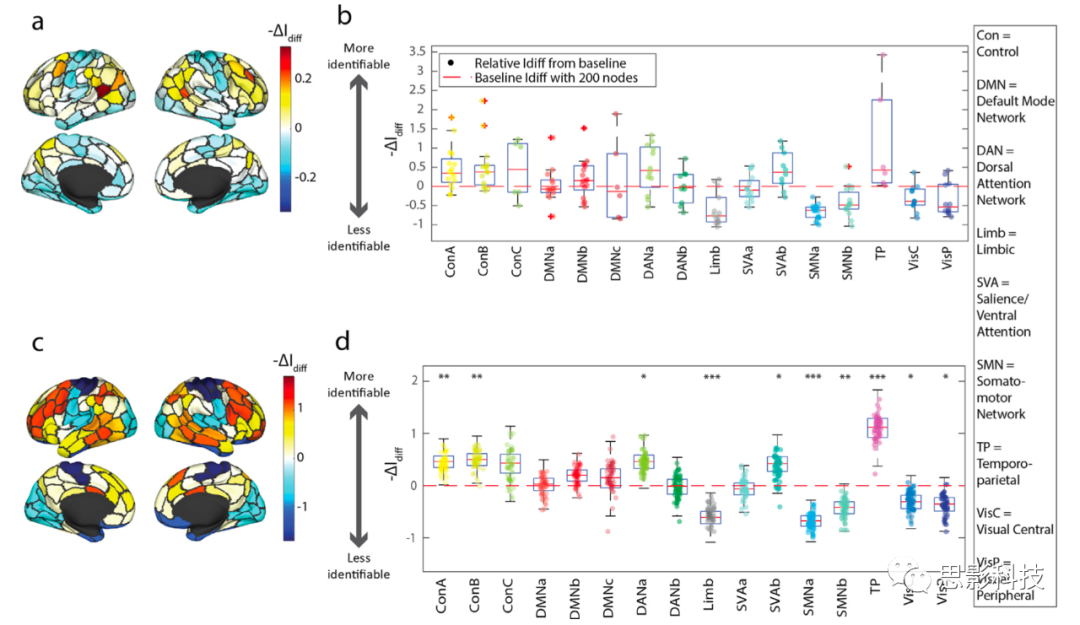 
(a)为了评估脑区对Idiff的贡献，我们计算了去除每个节点（N=200）上的所有连边后Idiff的变化。这里显示了投射到皮层表面的Idiff变化。
(b)我们根据大脑系统绘制了在计算eFC之前删除每个节点对Idiff的相对影响。
(c)在构建eFC之前排除整个系统的节点，揭示了特定系统对Idiff的正面或负面影响，并且(d)与随机去除匹配数量的节点相比，对Idiff有明显不同的结果(Bonferroni校正的p值；* = p < 0.003, ** = p < 0.0006, *** = p < 0.00006)。为了直观的展示结果，我们将ΔIdiff倒置为-ΔIdiff，它量化了一个节点的移除对整体Idiff的相对影响。如果一个节点的移除导致Idiff的降低，这个节点对识别能力的贡献将被认为是"增加Idiff"。
接下来，我们测试了与随机删除匹配数量的节点相比，哪个系统的节点对识别能力有显著影响（图3c-d）。通过随机排列系统标签（10,000次迭代），节点被随机地重新分配给系统。我们发现，当从控制A、控制B、背侧注意A、突显腹侧网络B和颞顶网络中删除节点时，识别能力比随机删除匹配数量的节点时明显降低（因此，图3d中这些系统的影响为正向的）。另外，我们发现与随机删除匹配数量的节点相比，删除边缘、躯体运动A和B、中枢和边缘视觉网络的节点会显著提高识别能力（因此，这些网络对Idiff相对负面的效应呈现在图3d中）。
综上所述，我们用节点留一法来揭示全脑识别能力的脑区驱动因素。我们发现包括额叶和颞上回有助于提高识别能力，而躯体运动、边缘和视觉区域则导致识别能力的降低。这些关于系统水平识别能力的结果在很大程度上与之前使用传统的、以节点为中心的功能连接的研究一致（Finn, Shen, Scheinost, Rosenberg, Huang, Chun, Papademetris, Constable, 2015, Mueller, Wang, Fox, Yeo, Sepulcre, Sabuncu, Shafee, Lu, Liu, 2013, Peña-Gómez, Avena-Koenigsberger, Sepulcre, Sporns, 2018），将大脑网络组织的特质定位到一个特定的系统子集。
2.3 eFC中系统和集群的识别能力
在前面的部分，我们证明了在一个足够长的fMRI扫描中，eFC的个体识别优于nFC，而且与单模态相比，多模态脑区有助于提高识别能力。在这里，我们继续研究整个大脑皮层识别能力的驱动因素，重点关注于eFC中每个大脑功能系统对识别能力的贡献。在本节中，我们旨在回答这些问题：来自单一系统的连边对识别能力有何贡献？集群连边的识别能力表现如何？
为了解决上述问题，我们首先只使用与特定大脑系统相关的连接对Idiff进行估计。对于nFC，这意味着只使用其代理节点（构成一条连边的两个脑区）被分配到同一大脑系统的连边来计算识别能力（Schaefer等人，2017）。我们使用eFC连边对进行了类似的操作，但要求与构成eFC条目的两条连边相关的所有四个节点被分配到同一系统。一般来说，我们发现eFC和nFC的系统特异的Idiff是高度相关的（R = 0.9578, p < 10-8；图4b）。我们报告了按Idiff排序的前五个和后五个系统。我们发现当节点都起源于颞顶、控制A、控制B、默认模式B和背侧注意B网络时，Idiff往往更大（图4a）。相反，我们发现，当节点来自躯体运动B、突显腹侧注意A、控制C、边缘视觉和边缘网络时，Idiff往往比较小（图4a）。我们注意到这些单系统的连边对（这里得单系统指的是两个连边涉及到的四个节点都来自一个系统）只代表eFC矩阵的一小部分（<1%），因此，这些结果只限于矩阵元素的子集。由于eFC包含了更广泛的连边对，其中一些涉及源自多达四个不同系统的节点，我们进一步分析了eFC在集群层面的情况。
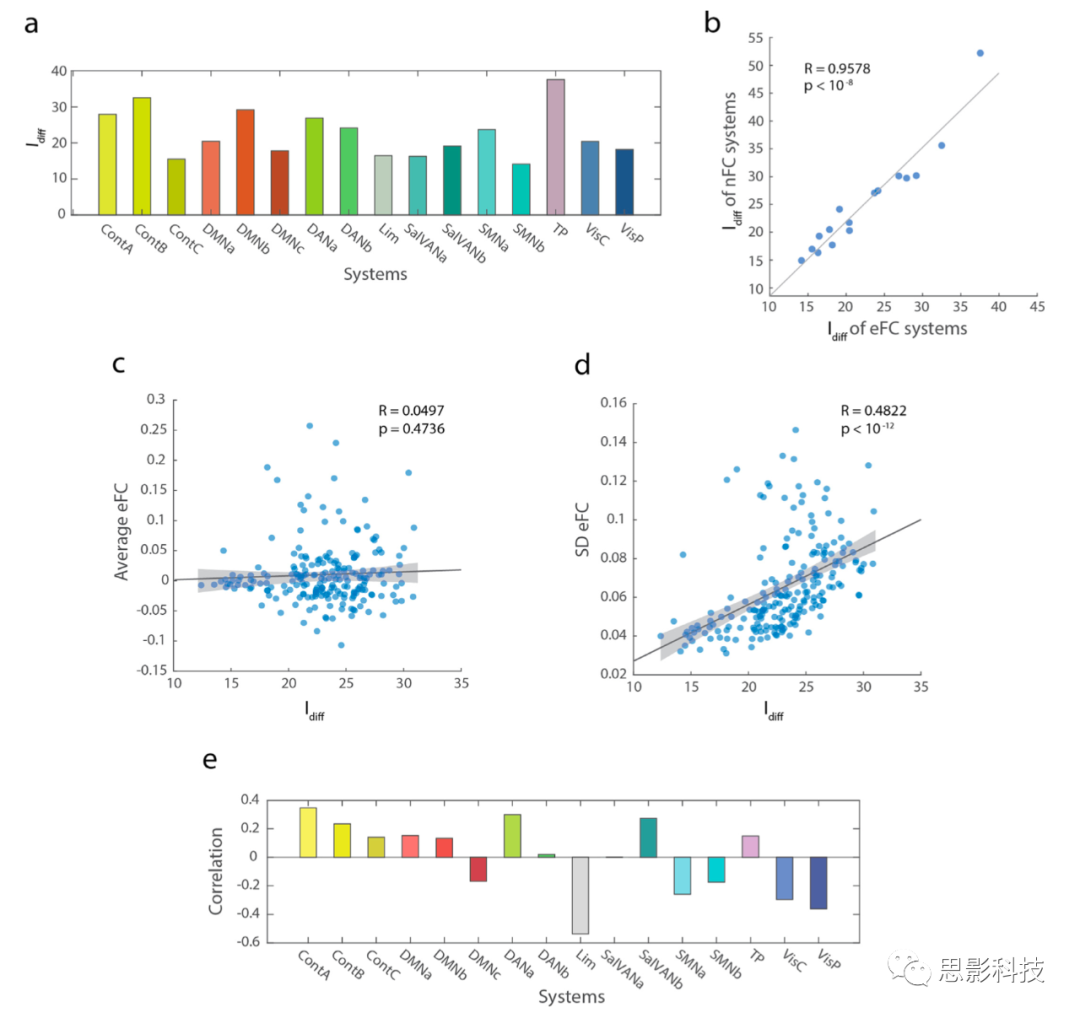
（a）显示了10个被试的10次rsfMRI扫描的系统eFC的被试内减去被试间的相似性。
（b）系统eFC和nFC的识别能力之间的高度相关性。
(c) Idiff与每个集群的eFC平均值不相关，但(d)每个集群的eFC值的标准差与Idiff明显相关。灰色阴影显示了95%的置信区间。
(e)16个典型的大脑系统Idiff与eFC集群的相关性。所有的分析都是使用MSC 200节点分区法进行的。
为了调查节点来自不同系统或集群的连边对的Idiff，我们使用标准的k-means算法，利用欧氏距离对eFC矩阵进行了聚类，聚类的数量从k=2到20。为此，我们首先对组平均eFC矩阵（所有扫描和被试的平均值；图S4a-b）进行了特征分解。我们保留前50个成分，然后将其作为k-means聚类算法的输入（图S4c）。对于一定数量的聚类k，我们重复了250次算法（图S4d）。从这250次估计中，我们保留了一个有代表性（即平均来看与其他分区最相似）的分区（图S4e）。这个程序的结果是将每一个k的连边划分为不重叠的社区。需要注意这个聚类程序是使用组平均eFC矩阵进行的，它可以与跨被试的集群相匹配。
然后我们将eFC矩阵的属性与识别能力联系起来。具体来说，我们使用组代表集群将连边-连边连接划分为"区块"，（这里指的是集群内和集群间的连边对）这些区块位于成对的社区之间（图S4f）。然后，对于每个区块，我们通过将这些权重表达为向量来计算所有扫描中这些连接的平均值和方差。接下来，我们用这些权重计算出所有个体和扫描对之间的相似度，并从这些相似度值中计算出该区块的识别能力。这些程序得到了每个区块的三个指标：
1）每个扫描矩阵的连边-连边连接的平均权重；
2）每个扫描矩阵的连边-连边连接的标准偏差；
3）使用所有扫描的连边-连边连接的皮尔逊相关的矩阵的识别能力。最后，对每个k聚类，我们计算这三个值在该聚类参与的所有区块上的平均值。然后，我们在图4c-d中绘制了识别能力与平均值和标准偏差值的关系。对于每个k，我们计算了"区块"的Idiff（图4）。
涉及每个集群的所有区块的Idiff的平均值和标准差被计算为每个集群的代表值。这个过程产生了图4c-d中的209个点（k = 2-20）。具体来说，我们发现一个集群的平均eFC与它的Idiff（R = 0.0497，p = 0.4736；图4c）不相关。此外，与某一聚类相关的eFC权重的平均变化率与Idiff（R = 0.4822，p < 10-12；图4d）呈正相关。这些区块指的是当eFC被集群标签重新排序时，集群内的连边-连边权重（图S4f）。
每个区块都对应于分配给不同聚类的连边之间的一组连边-连边连接（eFC）。对于每个区块，我们计算了连边-连边连接的平均数和标准差，这代表了分布的中心趋势和变化性。我们发现连边-连边连接的平均权重与识别能力没有显著关系。然而，一个区块内的连边-连边连接的变异性与较高的个体识别能力显著相关。我们还发现了nFC（k = 2-20）的聚类结果及其与Idiff的关系（图S5）。与使用eFC得出的结果不同（平均值：R = 0.0497，p = 0.4736；标准差：R = 0.4822，p < 10-12），我们发现在nFC时只有较弱的相关模式（平均值：R = 0.1392， p = 0.0444；标准差：R = 0.1494，p = 0.0309）。
哪些系统可能导致了高水平的Idiff ？为了解决这个问题，我们计算了每个系统在一个给定的集群中被代表的频率，并为每个大脑系统分别计算了这个频率与Idiff的相关性。我们发现，集群中的控制、默认模式A和B、背侧注意、突显腹侧注意和颞顶网络节点与集群的Idiff呈正相关。集群中的边缘、默认模式C和感觉运动系统（躯体运动和视觉）与Idiff的减少有关（图4e）。
总之，这些结果表明，在eFC中，高阶的认知系统，如控制、注意和默认模式网络，有助于提高个体识别能力，而感觉运动和边缘网络会降低个体识别能力。正如上一节所述，这些结果与之前使用nFC的分析相一致，都证明类似的系统和脑区促进了个体识别能力的增强（Finn, Shen, Scheinost, Rosenberg, Huang, Chun, Papademetris, Constable, 2015, Mueller, Wang, Fox, Yeo, Sepulcre, Sabuncu, Shafee, Lu, Liu, 2013）。此外，我们的结果表明，连接权重的内在异质性和可变性可能是解释为什么某些系统与较高或较低的个体识别能力相关的一个基本原因。
2.4 使用PCA重构的eFC提高了个体识别能力
本研究中我们着重使用完整的eFC矩阵或其连边-连边连接的特定子集进行Idiff的计算。作为最后的分析，我们想测试是否可以通过使用相对较少的主成分优化重建eFC来提高差异识别能力。
以前的研究使用了nFC的主成分分析（PCA）来提高识别能力（Amico, Goñi, 2018, Bari, Amico, Vike, Talavage, Goñi, 2019）。简而言之，该程序需要将所有被试和扫描的nFC（在本文是eFC）串联成一个按元素扫描的单一矩阵，将该矩阵分解为其主成分（PC），并通过逐渐包括越来越多的PC（按其特征值的降序）来重建eFC。在每次矩阵重建之前和重建之后，我们都会计算每次增加PC到每次扫描的eFC的Idiff。在此，我们将这一技术应用于MSC数据集中的nFC和eFC。
使用这种重建方法，我们发现nFC和eFC的Idiff都可以被优化。在nFC和eFC中，Idiff在k=10的成分上达到了峰值（对应于被试数量），eFC在识别能力上优于nFC（与Idiff = 21.17相比，峰值为Idiff = 35.27；图5b和e）。重测比较中也发现了这些结果（图S8）。那么，为什么在对识别能力进行优化时，PC的数量会与被试的数量相匹配？我们首先测试了每个被试的扫描次数对最大识别能力的PC数量的影响。当从100个被试中测试每个被试的两次扫描（图S7c）和从10个被试中随机选择的两次扫描（图S7a）时，优化识别能力所需的PC数量与数据集被试数量相符。当我们对整个HCP数据集（N = 100，每个被试两次扫描；图S7e）和将HCP数据集的扫描长度（2400个时间点）与MSC数据集（800个时间点；图S7f）相匹配时，这些结果可以重现。
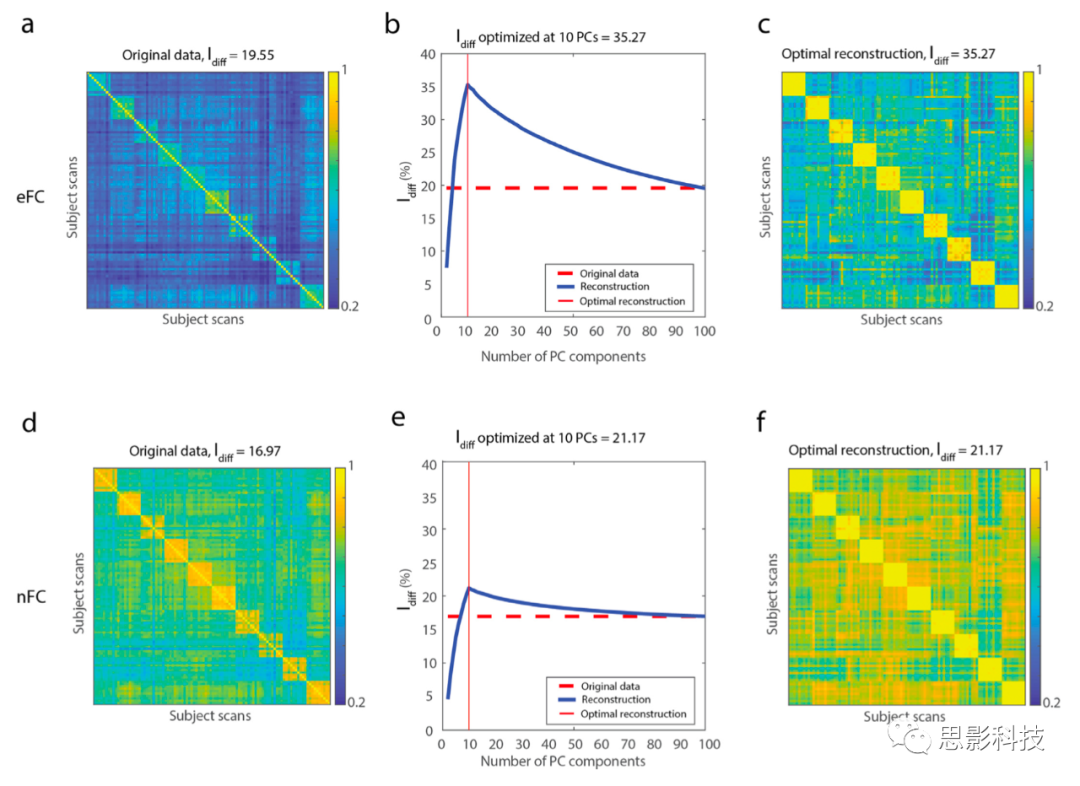
(a)在PCA（原始数据）之前eFC的扫描间相似性（皮尔逊相关）矩阵。
(b)当PC = 10时的最佳Idiff值；红色虚线是Idiff的原始值。
(c)为了最大的Idiff，使用10个PC重建eFC输出矩阵。
(d)PCA之前(原始数据)nFC的扫描间相似性(Pearson相关性)矩阵。
(e)当PC = 10时的最佳Idiff值，红色虚线是Idiff的原始值。
(f)为了最大的Idiff，使用10个PC重建nFC输出矩阵。
随后，我们探究了可以提高（PC = 1-10）或降低（PC = 11-100）识别能力的PC系数。第一主成分（PC1），从数学角度解释了eFC值跨扫描和跨被试的最大差异。PC1是唯一一个系数统一为正的成分（图S9）。接下来的九个系数（PC = 2-10）表现出了对应于单个被试的团块样的模式（图S9），而这种模式在PC = 11-100（图S10，图S11，图S12）中没有出现。
与之前的报告一致（Amico, Goñi, 2018, Rajapandian, Amico, Abbas, Ventresca, Goñi, 2020），我们的结果表明，通过有选择地保留与数据集中的被试数量相匹配的成分子集，可以提高个体识别能力。我们发现与nFC相比，使用eFC的改进幅度要大得多，这表明与nFC相比，eFC可以更好地捕捉个性化和特异性特征（Svaldi, Goñi, Abbas, Amico, Clark, Muralidharan, Dzemidzic, West, Risacher, Saykin, et al., Svaldi, Goñi, Sanjay, Amico, Risacher, West, Dzemidzic, Saykin, Apostolova, 2018）。
如您对脑功能或其他模态脑影像数据处理感兴趣，请浏览思影以下链接（直接点击即可浏览），感谢转发支持。(可添加微信号siyingyxf或18983979082咨询)：
上海：
第三十一届磁共振脑网络数据处理班（上海，10.28-11.2）
第六十九届磁共振脑影像基础班（上海，11.4-9）
第十四届任务态功能磁共振数据处理班（上海，11.30-12.5）
重庆：
第七十届磁共振脑影像基础班（重庆，10.22-27）
第二十八届弥散成像数据处理班（重庆，11.5-10）
第六届弥散磁共振成像提高班（重庆，11.17-22）
第二十三届磁共振脑影像结构班（重庆，11.27-12.2）
南京：
第三十三届磁共振脑网络数据处理班（南京，10.16-21）
第二十二届磁共振脑影像结构班（南京，10.24-29）
第七十一届磁共振脑影像基础班（南京，11.12-17）
第二十九届弥散成像数据处理班（南京，11.19-24）
北京：
第十届脑网络数据处理提高班（北京，10.20-25）
第十一届磁共振ASL（动脉自旋标记）数据处理班（北京，11.3-6）
第七十二届磁共振脑影像基础班（北京，11.9-14）
第六届影像组学班（北京，11.25-30）
数据处理业务介绍：
思影科技脑结构磁共振成像数据处理业务（T1)
思影科技定量磁敏感（QSM)数据处理业务
思影数据处理业务三：ASL数据处理
思影科技脑影像机器学习数据处理业务介绍
招聘及产品：
思影科技招聘数据处理工程师 （上海，北京，南京）
BIOSEMI脑电系统介绍
目镜式功能磁共振刺激系统介绍
3 讨论
3.1 连边功能连接增强了个体识别能力
本文的核心是观察到相对于传统的基于节点的连接nFC，eFC能提高个体识别能力。nFC测量两个脑区之间活动的相似性-一阶相关（Owen等人，2019），eFC测量连边对之间共同波动的相似性-高阶相关（Faskowitz等人，2020）。了解网络的高阶组织已在其他学科中被证明很有用（Ahn, Bagrow, Lehmann, 2010, Evans, Lambiotte, 2009, Nepusz, Vicsek, 2012, Trinh, Kwon, 2016）。本文从以连边为中心的视角，使我们能够将高阶的大脑网络组织与学科的具体特征联系起来。
eFC作为一个高阶的重建是否会导致个体识别的提高。即，如果我们要研究全脑nFC和eFC的识别能力，基于个体的连接数据，eFC是否能让我们更准确地识别一个独立个体？我们还好奇使用eFC的识别是否会受到扫描长度和数据量的影响。总的来说，我们发现如果有足够的数据量（大约800个时间点或30分钟），eFC在识别能力方面优于nFC。另外，我们注意到使用eFC计算的Idiff在使用串联扫描的情况下会达到更大的Idiff。这一结果可能反映了eFC的高阶性质。实际上，eFC测量的是相关性的相关性，比nFC需要更多的数据来获得一个稳定的估计（Bourin和Bondon，1998）。我们的结果表明随着这一估计的稳定，eFC可能比nFC在编码个性化和特异性特征上有优势。
接下来，差异识别能力（Amico和Goñi，2018b）是一个被试内扫描相似性与被试间扫描相似性相比的总结性指标，我们对其进行了测量。虽然其他自相似性指标如皮尔逊相关（Finn等人，2015）和I2C2（Shou等人，2013）已经稳健地识别了被试，Idiff也考虑到了被试间扫描相似性（Bridgeford等人，2020）。因此，一个高度可识别的扫描不仅是自相似的，而且还与其他被试的扫描不同。我们注意到，基于如何计算Idiff，相对于被试数量，每个被试的扫描次数可能会对Idiff造成偏差。这使得不同数据集的Idiff难以进行直接比较和解释。我们还发现跨I2C2、Discriminability以及Idiff在MSC 100和HCP 100节点数据集的基准测试中Idiff显示出最高的个体识别水平（图S13）。
我们的结果在两个数据集和两个不同的分区中得到了重现。这些结果表明高阶网络结构承载着重要的个体特定信息，因此，以连边为中心的方法可以更好的捕捉网络的特异性特征。这些观察结果既挑战也扩展了当前关于个体识别和精确网络映射的知识。我们的结果进一步倡导对深度表型的探究，这需要更多来自个体的数据。未来需要调查了解扫描长度（数据量）和高阶大脑表征之间的关系，如eFC（Owen等人，2019）。
3.2 多模态脑区驱动个体识别
哪些大脑区域驱动了eFC的个体特异性？是否有特定的大脑区域使被试更容易或更难被识别？为了回答这些问题，我们在三个不同的尺度上分析了个体识别能力。首先，我们用节点留一法分析了每个节点对Idiff的贡献。我们发现，当在构建eFC矩阵之前删除某些节点时，会导致Idiff明显减少或增加。特别是来自高阶系统的节点和连边导致Idiff明显的减少，而那些与感觉运动和边缘区域相关的节点和连边在构建eFC前被移除时导致了更高的识别能力。这些发现支持了早期的nFC结果，相比于单模态和初级感官脑区，高阶、多模态功能的脑区，包括额叶、顶叶和颞叶区域驱动了个体识别（Finn等人，2015）。
为什么多模态脑区可能有助于加强识别能力？一个可能的解释是与它们的多功能性有关。控制和颞叶网络中的区域被认为支持各种认知和心理过程，而这些过程是具有个体差异的。这些区域的功能连接模式方面在不同的被试之间有很大的差异（Mueller等人，2013年），是大脑皮层在进化过程中最晚扩展的部分（Sepulcre等人，2010年），属于生命中最晚发展的部分，因此可能是由早期生活经验形成的（Elston等人，2009年）。综上所述，观察到多模态脑区驱动个人的功能指纹特征，可能是认知、发育和进化过程的综合影响。然而，这些过程的确切机制还不清楚，应该是未来调查的目标。
然后我们探究了较高和较低的Idiff是否是来自单一典型大脑系统的连边对导致的（Schaefer等人，2017）。为了解决这个问题，我们从只使用16个大脑系统中的一个大脑系统构建的连边对中，分别估计了被试的eFC矩阵。我们发现，来自单系统的eFC和nFC的识别能力是明显正相关的，而且从多模态脑区形成存根的连边往往具有较高的Idiff。换句话说，单一系统内的内聚连边对不可能导致全脑范围的eFC的提高。相反，它表明落在不同脑网络之间的连边可能是驱动eFC中Idiff高于nFC的原因。
来自节点留一法和单一系统Idiff的结果表明，特定的大脑区域，即那些参与高阶大脑功能的区域，驱动着个体识别。在功能连接研究中发现这些高阶关联区域显示出最高的被试间差异（Miranda-Dominguez, Mills, Carpenter, Grant, Kroenke, Nigg, Fair, 2014, Mueller, Wang, Fox, Yeo, Sepulcre, Sabuncu, Shafee, Lu, Liu, 2013）。相关联脑区的功能连接已被发现在进化上是最新的（Zilles等人，1988），涉及智力（Choi, Shamosh, Cho, DeYoung, Lee, Lee, Kim, Cho, Kim, Gray, et al., 2008, Cole, Yarkoni, Repovš, Anticevic, Braver, 2012），一旦受到干扰，会导致神经精神障碍（Fornito, Harrison, 2012, Greicius, 2008）。另外，据报道，使用nFC对个体的高阶脑区的进行识别，可以预测流体智力（Amico, Goñi, 2018, Finn, Shen, Scheinost, Rosenberg, Huang, Chun, Papademetris, Constable, 2015）。综合来看，我们的结果显示，个体识别能力和高阶功能都源于多模态脑区，表明特异性的功能可能来自此类脑功能。
eFC和nFC矩阵中的顶点和连接数相差了几个数量级。为了匹配它们的维度确保更公平的比较，我们将nFC和eFC矩阵聚类为相同数量的社区。我们发现，连边-连边连接的方差与个体识别呈正相关，而这些连接的平均权重则没有。然而，我们发现使用组平均的nFC矩阵得到的关系相对较弱。因此，我们的结果进一步表明，eFC中连边-连边连接的差异性是个体识别能力的一个重要特征。我们还发现，与由与单模态大脑系统的连边组成的集群相比，包含起源于多模态系统连边的集群的识别能力水平更高。这些结果与nFC研究的结果（Finn, Shen, Scheinost, Rosenberg, Huang, Chun, Papademetris, Constable, 2015, Peña-Gómez, Avena-Koenigsberger, Sepulcre, Sporns, 2018）以及最近涉及eFC集群的研究（Jo等人，2020）一致。我们的研究结果表明，系统和集群内连接权重的变化可能是驱动连接组指纹和识别能力的一个重要特征。
在我们的分析中，我们使用了来自100和200个节点的Schaefer分区（Schaefer等人，2017）的Yeo17功能脑网络（Thomas Yeo等人，2011）。虽然Schaefer图集提供了一个从100到1000个节点的递增可扩展的分区，但由于计算上的限制，没有对Schaefer进行更细的分区以进行差异识别能力和后续分析。根据图S1的结果，在MSC和HCP数据集中，eFC比nFC在100和200节点分区中更容易识别。然而，随着节点数从100个增加到200个，识别能力的绝对差异减少了。需要进一步的分析来测试更细的分区中的个体识别能力，这最终可能导致eFC和nFC的Idiff达到一个峰值。包括两种模式的大脑功能网络表征的多模式方法可能被用来计算最大的个体识别能力。需要进一步的研究以确定在测量识别能力方面的分区和元素数量的影响。
总的来说，我们的研究结果表明个体识别是由来自高阶大脑系统的多模态脑区驱动的。这些观察结果对生成具有被试特定信息的稳健的网络生物标志物有明显的影响，同时将所需的数据量减少到其子集。更重要的是，我们的研究结果表明，具有高方差的eFC集群，也许在组水平的分析中被削弱，但可能用于确定被试的特定信息或个性化医疗。另外，这项研究为未来关于任务的生物标志物提供了线索，该研究可用于进一步明确在fMRI采集过程中任务对识别能力的影响，并且在不要求扫描长度的情况下最大限度地提高被试的特异性，特别是对于脆弱和临床人群（Laumann等人，2015年）。最后，eFC矩阵的聚类在不同的被试中的结果是稳健的，显示出作为一种降维方法的潜力。未来的工作有必要明确对组水平和个体水平大脑网络具有鲁棒性的集群或连边子集，并解释被试间特异性和大脑的eFC是否受任务状态的调节。
3.3 主成分分析突出了eFC的特殊性
在这里，我们遵循最新的nFC研究，将PCA应用于eFC数据，有效地将eFC还原为一组小的主成分（Amico, Goñi, 2018, Bari, Amico, Vike, Talavage, Goñi, 2019）。我们发现，只用那些能解释最大方差的成分选择性地重建eFC，可以提高被试的识别能力，优化的程度远远超过对nFC数据采用相同程序时的表现。这表明，基于完全相同的fMRI BOLD数据，eFC数据具有更强的个体水平的指纹识别能力。我们注意到，其他方法，如跨被试的相关矩阵的z-score归一化，也增加了被试内与被试间扫描相似性的绝对差异（Finn等人，2015）。未来还需要进一步研究，以从给定的数据集中最大限度地获得特定被试信息。
有趣的是，用于优化eFC的个体识别能力所需的PC数量与两个独立数据集中的被试数量相匹配。这些结果与之前使用nFC进行个体识别的研究相符（Amico和Goñi，2018b）。我们的结果还显示尽管一个被试有超过一对重测的rsfMRI扫描，但这是稳健的。那么，为什么在对识别能力进行优化时，PC的数量与被试的数量相匹配？为了解决这个问题，我们分析了增加（PC = 1-10）或降低（PC = 11-100）识别能力的PC的系数。从数学角度解释了eFC值跨扫描和跨被试的最大差异。这是100个主成分中唯一具有持续正值的PC。另外，只有PC从2到10对特定被试的扫描显示出明显的区块样模式。一种可能性是，第一个PC解释了组水平的eFC变异，即潜在的组水平的eFC特征，而PC2到10倾向于解释个体级eFC变异。我们推测，PC的数量是N-1（N=被试的数量），因为每个被试都可以通过消除的过程来确定N-1个PC。这些结果进一步证明，在用线性转换算法（如PCA）研究和改善个体识别能力时，eFC可以是一个有价值的方法。然而，未来的工作有必要宣传PC的精确特征，并应探索其他降维方法如因子分析或CCA（Child, 1990, Thompson, 1984）来优化Idiff。
3.4 展望
我们的结果为未来的研究提供了令人兴奋的可能性。在这里，我们使用了一个以前定义的识别能力。然而，这个衡量标准在某些情况下可能会产生误导。例如，如果大多数被试表现出高水平的自我相似性，即使其余的被试表现出较差的自我相似性，Idiff仍然可以取得高值（Abbas, Amico, Svaldi, Tipnis, Duong-Tran, Liu, Rajapandian, Harezlak, Ances, Goñi, Abbas, Liu, Venkatesh, Amico, Harezlak, Kaplan, Ventresca, Pessoa, Amico, Goñi, 2018, Jalbrzikowski, Liu, Foran, Klei, Calabro, Roeder, Devlin, Luna, 2020）。未来的工作应该研究量化个体识别程序性能的替代方法，包括组内相关系数（I2C2）（Shou等人，2013）和Discriminability（Bridgeford等人，2020）。此外，未来的工作应该探索个体识别的多变量方法（Yoo等人，2019）。
还应通过跟踪识别能力在整个发展和系统发育过程中的变化来发现关于识别能力的起源问题。具有高水平识别能力的区域表现出明显的跨物种差异（Xu等人，2020年），在人类的一生中始终具有特异性（Jalbrzikowski等人，2020b），受遗传影响（Demeter等人，2020年），并在大鼠动物模型中具有高度识别能力（Bergmann等人，2020年）。了解识别能力和基于连接的特异性的起源，可以帮助我们了解心理病理学、大脑进化以及发育和衰老过程。
机器学习技术的应用（Demeter等人，2020年），结合各种成像模式（Kumar等人，2018年），以及增加fMRI分区的颗粒度（Tipnis等人，2020年）已被发现能有效改善个体识别能力。只关注那些最大限度地提高被试特异性的神经元素（Sripada等人，2020年）或选择性地使用高振幅的"事件"时间框架重建eFC，这在以前的工作中改善了nFC的识别能力（Esfahlani等人，2020年），这些方法可能有助于减少提高eFC识别能力所需的数据量和计算资源。未来的研究需要最大限度地利用eFC从有限的fMRI扫描时间和计算资源中发现特异性特征。
3.5 局限性
与eFC相关的一个限制是将其与个别脑区联系起来。eFC矩阵中的每个连接总是涉及四个节点（两个连边-连边连接），在大多数情况下，将其分配给任何一个脑区或认知系统是不可能的。在此，我们避免了这一复杂问题，从所产生的eFC的识别能力中测量了一个节点的移除（相当于200个节点分区中的199条边）的影响，并且只考虑了来自单一系统的连边对。虽然这些方法试图将连边定位到大脑区域，但未来的工作有必要确定一个强大的方法，将eFC元素追溯到大脑的特定位置。
第二个限制是关于"差异识别能力"的测量方法，它同时考虑了被试内和被试间的相似性。然而，我们承认识别能力的其他指标，如计算FC-FC相关性的个体识别精度（Finn等人，2015年），ROC（受试者工作特征）曲线精度（Jalbrzikowski等人，2020a），以及在图形嵌入表示中对每个被试使用最邻质心分类模型（Abbas等人，2020a）。尽管如此，我们还是使用Idiff进行分析，因为这种方法扩展了一种流行的识别方法（Finn等人，2015），同时考虑到了不同被试之间共享的"共同特征"（Amico和Goñi，2018b）。然而，其他测量识别能力和比较fMRI数据的方法也应该被调查和开发，以进一步了解以连边为中心的FC的特异性。
最后一个限制是关于估计连边聚类和利用其结果的程序。在这里，我们使用k-means算法，根据eFC的相似度将连边划分为一组固定数量的集群。这种估计连边集群方法的好处是计算效率高，可以用距离度量来计算。基于聚类的替代方法有很多（Fortunato，2010，Porter，Onnela，Mucha，2009，Sporns，Betzel，2016），必须开发其他算法来检测连边集群。另外，集群之间的连边可能作为功能系统之间的桥梁，以进一步解释特异功能和行为之间的关联（Jo等人，2020）。然而，我们的分析排除了集群之间的连边，而专注于集群内的连边。未来的研究应该调查不同聚类算法的影响，并研究聚类内连边与聚类间连边对个体差异的影响。
4 材料和方法
4.1 数据集
The Midnight Scan Club（MSC）数据集（Gordon等人，2017年）包括10名成年人（女性占50%，年龄=29.1±3.3）的rsfMRI数据。该研究得到了华盛顿大学医学院人类研究委员会和机构审查委员会的批准，并得到了所有被试的知情同意书。每个被试的12次扫描是在不同时间获取的。对于每个被试，使用梯度回波EPI序列（运行时间=30 min，TR=2200 ms，TE=27 ms，翻转角=90°），进行10次rsfMRI扫描，同时对被试进行眼球追踪以监测长时间闭眼的情况（用于评估嗜睡情况）。图像是在3T西门子Trio机器上收集的。
The Human Connectome Project（HCP）数据集（Van Essen等人，2012年）包括 来自100名无关联的成年被试（女性占54%，平均年龄=29.11±3.67，年龄范围=22-36）的静息态功能数据。这些被试是由人类连接组计划发布的“100 Unrelated Subjects(U100)”中选出的。该研究得到了华盛顿大学机构审查委员会的批准，并获得了所有被试的知情同意书。被试在两天的时间里接受了四次15分钟的rsfMRI扫描。关于成像参数和图像预处理流程的完整描述可以在Glasser等人发表的文献（2013）中找到。使用梯度回波EPI序列采集rsfMRI数据（运行时间=14:33 min，TR=720 ms，TE=33.1 ms，翻转角=52°，各向同性体素分辨率为2 mm，多频带因子=8），被试睁眼并固定在一个十字架上。图像是在带有32通道头部线圈的3T西门子Connectome Skyra机器上收集的。
4.2 图像预处理
4.2.1 MSC功能数据预处理
使用基于Nipype 1.1.9（Gorgolewski等人，2011）的fMRIPrep 1.3.2（Esteban等人，2017）对MSC数据集中的功能图像进行预处理（fMRIPrep是融合了FSL, AFNI, freesurfer,ants的pipeline）。以下对fMRIPrep预处理的描述是基于随软件分发的模板，该软件由"不保留权利"（CCO）许可证覆盖。fMRIPrep的内部操作包括Nilearn 0.5.0（Abraham等人，2014）、ANTs 2.2.0、FreeSurfer 6.0.1、FSL 5.0.9和AFNI v16.2.07。关于该pipeline的更多细节，见fMRIPrep文档中与工作流程对应的部分。
每个被试的T1加权(T1w)图像使用N4BiasFieldCorrection (ANTS)（Avants, Epstein, Grossman, Gee, 2008, Tustison, Avants, Cook, Zheng, Egan, Yushkevich, Gee, 2010）进行强度不均匀性校正，并在整个处理流程中用作T1w参考。然后使用antsBrainExtraction.sh工作流的Nipype实现颅骨剥离，使用NKI作为目标模板。使用recon-all（Dale等人，1999年）重建大脑表面，并使用Mindboggle（Klein等人，2017年）来完善之前估计的大脑掩模，以调和ANTs和FreeSurfer衍生的皮层灰质分割。使用T1w体积和模板提取的大脑进行非线性配准(antsRegistration)，空间标准化到ICBM 152非线性非对称模板(2009c)。使用FSL fast对提取的T1w进行脑脊液(CSF)、白质(WM)和灰质(GM)的脑组织分割（Zhang等人，2001）。
使用AFNI的3d Tshift对功能数据进行时间层校正，使用FSL的mcflirt进行头动校正。通过对同一被试的功能图像进行共配准，进行无场图失真校正。基于antsRegistration，使用平均场图模板限制强度翻转的T1w图像。然后采用基于边界的共配准方法（9个自由度）对相应的T1w进行配准。将运动校正变换、场失真校正扭曲、BOLD-T1w变换和T1w-MNI模板扭曲统一在antsApplyTransforms的Lanczos插值步骤中应用。根据上述预处理过程产生的BOLD逐帧位移（FD）、DVARS和三个区域性全局信号，计算出几个混杂的时间序列。FD和DVARS是为每个功能运行计算的，都是通过Nipype实现。三个全局信号是在CSF、WM和全脑掩模中提取的。本研究中使用的每个MSC被试的NIFTI结果文件遵循文件命名模式：*_spaceT1w_descpreproc_bold.nii.gz。
4.2.2 HCP功能数据预处理
根据Glasser等人（2013）的描述，对HCP数据集中的功能图像进行了最小化的预处理。简而言之，这些数据被校正了梯度失真和运动失真，然后通过一个样条插值步骤与相应的T1加权（T1w）图像对齐。这个容积被进一步校正了强度偏差，并归一化为10,000的平均值。然后将该容积投射到32k_fs_LR网格，排除异常值，并使用多模态表面配准（Robinson等人，2014）对准一个公共空间。本研究中使用的每个HCP被试的结果CIFTI文件遵循文件命名模式：*_REST{1,2}_{LR,RL}_Atlas_MSMAll.dtseries.nii。
4.2.3 图像质量控制
所有来自MSC和HCP数据集的功能图像都被保留。使用fMRIPrep的视觉报告和MRIQC 0.15.1（Esteban等人，2017）评估MSC中功能图像的质量。通过肉眼检查MSC数据的全脑视野覆盖、信号伪影、以及与相应的解剖图像的正确对齐情况。所有的时间序列数据也进行了验视。
4.3 功能网络预处理
4.3.1 分区预处理
一个旨在优化fMRI信号的局部梯度和全局相似性测量的功能分区方法（Schaefer等人，2017）（Schaefer200）被用来定义大脑皮层上的200个区域。这些节点也被映射到Yeo典型功能网络（Thomas Yeo等人，2011）。对于HCP数据集，Schaefer200在32k_fs_LR空间以CIFTI文件的形式公开提供。对于MSC数据集，使用高斯分类器表面图集（Fischl等人，2004）（在100个不相关的HCP被试上训练）和FreeSurfer的mris_ca_label函数，每个被试都有一个Schaefer200分区。这些工具利用在recon-all pipeline中计算的表面配准，根据个体表面曲率和沟回模式，将群体平均图谱转移到个体空间。这种方法为每个被试呈现了一个T1w空间体积。为了与功能数据一起使用，分区的部分被重新取样到2 mm的T1w空间。这个过程可以重复用于其他分辨率的分区（如Schaefer100）。
4.3.2 功能网络预处理
每个预处理的BOLD图像都使用Nilearn的signal.clean，进行线性去趋势、带通滤波（0.008-0.08Hz）（Parkes等，2018）、混淆去除和标准化，去除与时间滤波正交的混杂（Lindquist等，2019）。采用的混淆回归（Satterthwaite等，2013）包括6个运动估计值、平均CSF、平均WF和平均全脑信号的时间序列，这9个回归因子的导数，以及这18项的平方。此外，对于每帧超过运动阈值的fMRI图像（MSC=0.5 mm的帧间位移，HCP=0.25 mm的均方根位移），加入一个峰值回归因子。这种混淆策略已被证明是减少运动相关伪影的一个相对有效的选择（Parkes等人，2018）。经过预处理和回归噪声协变量，恢复了每个节点的残差平均BOLD时间序列。
4.3.3 连边图论构建
通过获取局部时间序列数据和它们的z-scores来计算eFC（就是对每个时间点的值做z变化，即标准化）。然后，对于所有成对的脑区，我们计算它们的z-scores时间序列的两个矩阵对应位置元素的乘积。这将得到"连边时间序列"，其元素表示大脑区域对之间的瞬时共波动的幅度，它的整个时间序列的平均计算结果是完全等于Pearson相关系数。最后，对连边时间序列对之间进行计算，获得这两条连边时间序列的共变关系。当在所有对的边上重复时，结果就会是一个逐边矩阵，其元素被归一化到区间[-1，1]。
4.3.4 差异识别能力
功能连接组的识别能力或指纹分析是基于以下假设，相比于不同被试之间，单个被试的连接情况应该与该被试的不同扫描和模块中更为相似。之前的研究使用传统功能连接组（Finn等人，2015年）表明，使用皮尔逊相关分析，从一组被试的FC中使用sample FC找到被试的"目标"FC，就可以对个体进行强有力的识别。之前关于量化功能连接的个体差异的研究包括计算测地距离（Venkatesh等人，2020）和个体扫描间的皮尔逊相关（Amico和Goñi，2018b）。虽然测地距离方法也提供了扫描间差异的总结性措施，但我们采用Amico和Goñi（2018b）的量化指标，该指标考虑了eFC和FC矩阵的协方差和标准偏差。这个度量被称为差异识别能力（Idiff），来源于"识别能力矩阵"，即被试FC之间的相关性（Pearson）矩阵。通过量化自我识别能力或Iself并且减去被试之间的相似性或Iothers来计算Idiff，表示为识别能力矩阵的对角线和非对角线元素（图1b）。一组被试的差异识别能力（Idiff）可以总结为以下几点：
为了测试重复性和分区的影响，我们用HCP数据集的100个无关联的被试重复进行了分析（Van Essen等人，2012）。HCP数据集包括每个被试在不同日期的两个扫描时段的四次扫描。对于每个时段，我们将两个扫描（从左到右和从右到左的相位编码）串联成一个具有代表性的时间序列。随后我们用这两个时间序列来测量被试内相似度Iself。通过测量100个和200个节点数据集的差异识别能力，测试了分区数量的影响（图S1）。
4.3.5 通过节点留一法追踪大脑区域的识别能力
在上一节中，我们描述了计算Idiff的流程，这是一个已知的量化被试内与被试间扫描的相对相似性的方法（Amico和Goñi，2018a）。在本节中，与使用整个eFC矩阵计算相比，我们测试了从eFC的计算中移除哪些脑区会减少个体识别的Idiff。此外，我们还测试了与使用全脑eFC相比，去除特定的大脑系统是否会明显减少Idiff。
eFC连边对的共同强度和脑区之间的直接联系在某种程度上可以是一个任意的程序，因为在eFC中一个连边对中最多可以有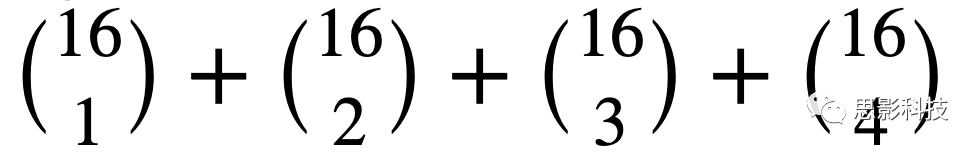
个脑区的组合。为了避免做出连边对的权重与连边对强度呈线性关系的假设，我们在构建eFC矩阵之前采用了节点留一法。在构建eFC之前去除一个节点的效果是通过从全脑Idiff中减去去除一个节点的eFC的Idiff来计算的（图3a-b）。
随后，我们检查了每个大脑功能系统的影响，以及如果去除该系统，从eFC测得的Idiff差异。类似于前面的单个节点去除方法，我们去除了单个系统（即单个系统的所有节点），并通过从全脑中Idiff减去这一结果来测量其对Idiff的影响（图3c-d）。我们没有控制节点数量的差异（即整个大脑是200个节点，单个系统去除的大约为190个节点），因为节点总数对Idiff的影响还不清楚。
4.3.6 单一系统连边对的识别能力
节点留一法的好处和注意事项是，由于eFC的重叠特性，它删除了所有涉及特定节点或系统的连边对（Faskowitz等人，2020）。因此，由于这一特点，我们仍不清楚纯粹的单一系统的影响。为了确定单一系统的Idiff，我们提取了只包括来自特定系统的节点的连边对并测量了Idiff。类似的方法被应用于nFC，其中包括来自nFC的节点对，这些节点包括来自单一系统的节点。单一系统的节点对与eFC的连边对进行了比较（Pearson相关性）。此外，使用来自单一系统的连边对的被试相似性矩阵包括见图S3。
4.3.7 识别能力的K-means聚类算法
与传统的nFC矩阵相比，这里使用的eFC矩阵具有成分维数的平方。虽然eFC的高维数可能有助于展示FC矩阵中无法直接显示的其成分之间的关系（连边之间的关联），但这对eFC矩阵的成分进行聚类是一个计算上的挑战。如果矩阵的分区数量未知，留待探索的话，情况就更严重了。为了解决这个问题并对eFC进行聚类，我们应用了一个简单的两步聚类程序，对eFC矩阵的低维形式进行操作。
首先，按照Faskowitz等人的研究（Faskowitz等，2020年），我们对平均eFC矩阵（19900 × 19900）进行了特征分解，该平均eFC矩阵由所有扫描的eFC矩阵的平均值创建，保留了与最大特征值相关的前50个特征向量。通过将每个特征向量除以其最大的幅度元素，这些特征向量被重新调整为[-1,1]区间内。然后，我们用标准的k-means算法和欧几里得距离对重新缩放的特征向量进行聚类。我们改变了社区的数量k，从k=2到20，在每个值下重复聚类算法250次。我们保留了与所有其他分区具有最大整体相似性的分区作为代表性分区。
我们使用k-means将连边划分为集群，数目从k=2到k=20（共209个不同的集群）。将eFC划分为k集群可以用来将相应的eFC矩阵划分为k个集群内和k(k-1)/2个集群间连边-连边相连的组块。我们的目的是利用这些组块的特征来更好地理解不同的集群和系统是如何与Idiff相关联的。这些步骤已在图S4中进一步阐述。
为此，我们进行了以下几项分析。首先，对于每个区块，我们提取每个被试和每次扫描的元素，并计算成对的相似性矩阵。如果该区块内的连边-连边连接的权重是相关的，就可以认为两次扫描是彼此相似的。然后，我们为每个区块计算其他几个特征。这些特征包括每个区块的连边-连边连接的平均数和标准差，以及每个大脑系统在分配给该区块的连边中的代表程度。简而言之，区块是从组平均eFC矩阵的集群中得出的。每个区块代表了成对的集群之间的连边-连边连接的集合。来自所有扫描和被试的每个区块的eFC元素被用来计算这个区块的eFC值的平均值和标准差。然后，对于每一个k集群，我们计算该集群的所有区块的平均数和标准差。最后，我们通过系统标签来计算每个区块的元素，我们发现这些系统标签与区块的Idiff有关。
在数学上，这些集群代表了不重叠的连边集群。我们发现也可以使用一些其他社区发现算法（社区发现算法用来发现网络中的社区结构，可以视为一种广义的聚类算法），如模块度最大化（Newman and Girvan, 2004）和Infomap（Rosvall and Bergstrom, 2008）。然而，在此考虑到实用性（即快速的运行时间），我们使用了k-means算法。
4.3.8 主成分分析
主成分分析（PCA）是一种广泛使用的可用于探索数据基本结构的统计方法（Jolliffe，2014）。PCA将一组具有潜在相关变量的观察数据转化为一组称为主成分的线性不相关变量。然后将这些主成分按照解释数据方差从大到小的顺序进行排序。我们采用主成分分析来直接对比eFC与nFC的识别能力表现，这点Amico和Goñi（2018b）已经进行了探索。
首先，主成分的数量与数据集中的功能连接组的数量进行匹配。根据定义，分解PCA可以解释数据中100%的方差。对从PC=2到20的PC按其解释的方差进行降序排列。个体的nFC和eFC随后被重建为所包含的成分数量的函数，其理由是组水平的信息在高方差成分中进行，而个体水平的信息则在较低方差成分中传达。在这个重建过程中，我们按照解释方差的递减顺序对PC进行了加和。在每次加法重建时，每个个体的连接矩阵都是根据PC=1到N的平均数和线性重组的PC来重建的。
接下来，我们控制了被试扫描次数的影响，它可以影响被试的总扫描时间或数据量（图2a，b）。从MSC数据集中，我们从每个被试的十次扫描中随机选择两次作为PCA衍生的Idiff最大值进行测试性扫描，进行100次迭代。在eFC和nFC中，用与数据集中的被试数量相匹配的10个PC优化Idiff。同时，我们从100个被试中随机抽出10个被试来测试是否Idiff可以优化被试数量，而不考虑被试本身。在HCP数据集中，我们从100个被试中随机选择了10个被试，每个被试有两次扫描。在100次迭代中的每一次，为每个PC的Idiff绘制了可视化的图（图S7c-d）。我们还通过匹配HCP数据集的时间点（2400个时间点）和MSC数据集的时间点（800个时间点；图S7f）的数量来测试扫描时间的影响。对于每个被试，我们只将从左到右和从右到左的扫描中的400个时间点连接来创建一个800个时间点的扫描。换句话说，两个扫描的中间部分被连接起来，为每个被试创造一个800个时间点的单一扫描数据。通过连接的扫描，我们进行了类似于图S7c的分析。最后，我们用整个HCP数据集（100个被试；每个被试两个扫描；图S7e）计算了PC重建后的Idiff。
在MSC和HCP数据集中，我们发现被试的数量与主成分的数量相匹配，主成分的Idiff在重建的eFC和nFC矩阵中是最大的。为了确定这一结果的潜在驱动因素，我们对每次扫描的每个PC系数进行了分解，图S9、图S10、图S11、图S12。对于PC从2到10，每个被试的系数与其他被试的系数进行了测试（t – test with Bonferroni-correction）。
如需原文及补充材料请添加思影科技微信：siyingyxf或18983979082获取,如对思影课程及服务感兴趣也可加此微信号咨询。另思影提供免费文献下载服务，如需要也可添加此微信号入群，原文也会在群里发布，如果我们的解读对您的研究有帮助，请给个转发支持以及右下角点击一下在看，是对思影科技的支持，感谢！
微信扫码或者长按选择识别关注思影
非常感谢转发支持与推荐
欢迎浏览思影的数据处理业务及课程介绍。（请直接点击下文文字即可浏览思影科技所有的课程，欢迎添加微信号siyingyxf或18983979082进行咨询，所有课程均开放报名，报名后我们会第一时间联系，并保留已报名学员名额）：核磁：
上海：
第三十一届磁共振脑网络数据处理班（上海，10.28-11.2）
第六十九届磁共振脑影像基础班（上海，11.4-9）
第十四届任务态功能磁共振数据处理班（上海，11.30-12.5）
重庆：
第七十届磁共振脑影像基础班（重庆，10.22-27）
第二十八届弥散成像数据处理班（重庆，11.5-10）
第六届弥散磁共振成像提高班（重庆，11.17-22）
第二十三届磁共振脑影像结构班（重庆，11.27-12.2）
南京：
第三十三届磁共振脑网络数据处理班（南京，10.16-21）
第二十二届磁共振脑影像结构班（南京，10.24-29）
第七十一届磁共振脑影像基础班（南京，11.12-17）
第二十九届弥散成像数据处理班（南京，11.19-24）
北京：
第十一届磁共振ASL（动脉自旋标记）数据处理班（北京，11.3-6）
第七十二届磁共振脑影像基础班（北京，11.9-14）
第六届影像组学班（北京，11.25-30）
脑电及红外、眼动：
重庆：
第二十七届脑电数据处理入门班（重庆，10.28-11.2）
南京：
第五届脑电机器学习数据处理班（Matlab版本，南京，11.3-8）
上海：
第三十六届脑电数据处理中级班（上海，11.13-18）
更新：第二十五届近红外脑功能数据处理班（上海，12.7-12）
北京：
更新：第十三届眼动数据处理班（北京，10.26-31）
数据处理业务介绍：
思影科技功能磁共振(fMRI)数据处理业务
思影科技弥散加权成像（DWI/dMRI）数据处理
思影科技脑结构磁共振成像数据处理业务（T1)
思影科技定量磁敏感（QSM)数据处理业务
思影科技啮齿类动物（大小鼠）神经影像数据处理业务
思影科技灵长类动物fMRI分析业务
思影数据处理业务三：ASL数据处理
思影科技脑影像机器学习数据处理业务介绍
思影科技微生物菌群分析业务
思影科技EEG/ERP数据处理业务
思影科技近红外脑功能数据处理服务
思影科技脑电机器学习数据处理业务
思影数据处理服务六：脑磁图（MEG）数据处理
思影科技眼动数据处理服务
招聘及产品：
思影科技招聘数据处理工程师 （上海，北京，南京，重庆）
BIOSEMI脑电系统介绍
目镜式功能磁共振刺激系统介绍
